
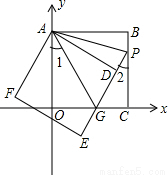
如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标(3,3),将正方形ABCO绕点A顺时针旋转角度α(0°<α<90°),得到正方形ADEF,ED交线段OC于点G,ED的延长线交线段BC于点P,连AP、AG.
(1)求证:△AOG≌△ADG;
(2)求∠PAG的度数;并判断线段OG、PG、BP之间的数量关系,说明理由;
(3)当∠1=∠2时,求直线PE的解析式.
(1)证明见解析;(2)∠PAG =45°,PG=OG+BP.理由见解析;(3)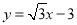 .
.
【解析】
试题分析:(1)由AO=AD,AG=AG,利用“HL”可证△AOG≌△ADG;
(2)利用(1)的方法,同理可证△ADP≌△ABP,得出∠1=∠DAG,∠DAP=∠BAP,而∠1+∠DAG+∠DAP+∠BAP=90°,由此可求∠PAG的度数;根据两对全等三角形的性质,可得出线段OG、PG、BP之间的数量关系;
(3)由△AOG≌△ADG可知,∠AGO=∠AGD,而∠1+∠AGO=90°,∠2+∠PGC=90°,当∠1=∠2时,可证∠AGO=∠AGD=∠PGC,而∠AGO+∠AGD+∠PGC=180°,得出∠AGO=∠AGD=∠PGC=60°,即∠1=∠2=30°,解直角三角形求OG,PC,确定P、G两点坐标,得出直线PE的解析式.
试题解析:(1)证明:∵∠AOG=∠ADG=90°,
∴在Rt△AOG和Rt△ADG中,
∵ ,
,
∴△AOG≌△ADG(HL);
(2)【解析】
PG=OG+BP.
由(1)同理可证△ADP≌△ABP,
则∠DAP=∠BAP,由(1)可知,∠1=∠DAG,
又∠1+∠DAG+∠DAP+∠BAP=90°,
所以,2∠DAG+2∠DAP=90°,即∠DAG+∠DAP=45°,
故∠PAG=∠DAG+∠DAP=45°,
∵△AOG≌△ADG,△ADP≌△ABP,
∴DG=OG,DP=BP,
∴PG=DG+DP=OG+BP;
(3)【解析】
∵△AOG≌△ADG,∴∠AGO=∠AGD,
又∵∠1+∠AGO=90°,∠2+∠PGC=90°,∠1=∠2,
∴∠AGO=∠AGD=∠PGC,
又∵∠AGO+∠AGD+∠PGC=180°,∴∠AGO=∠AGD=∠PGC=60°,
∴∠1=∠2=30°,
在Rt△AOG中,AO=3,OG=AOtan30°=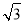 ,则G点坐标为:(
,则G点坐标为:(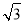 ,0),
,0),
CG=3-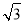 ,
,
在Rt△PCG中,
PC=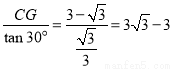 ,
,
则P点坐标为:(3,3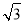 -3),
-3),
设直线PE的解析式为y=kx+b,
则 ,解得
,解得 ,
,
所以,直线PE的解析式为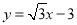 .
.
考点:一次函数综合题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:2015届山东新泰龙廷镇中心学校八年级下第一次月考数学试卷(解析版) 题型:解答题
如图,在△ABC中,D是边AB的中点,DE∥BC交AC于点E.求证:AE=EC
查看答案和解析>>
科目:初中数学 来源:2015届天津市河西区八年级下学期期末考试数学试卷(解析版) 题型:填空题
已知一次函数的图象经过点(2,3),且满足y随x的增大而增大,则该一次函数的解析式可以为 _________ (写出一个即可).
查看答案和解析>>
科目:初中数学 来源:2015届天津市河西区八年级下学期期末考试数学试卷(解析版) 题型:选择题
已知一次函数的图象过点(3,5)与(﹣4,﹣9),则该函数的图象与y轴交点的坐标为( )
A.(0,﹣1) B.(﹣1,0) C.(0,2) D.(﹣2,0)
查看答案和解析>>
科目:初中数学 来源:2015届北京市顺义区八年级下学期期末考试数学试卷(解析版) 题型:解答题
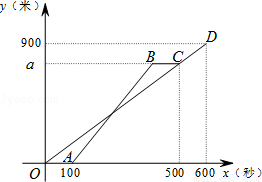
甲、乙两人从顺义少年宫出发,沿相同的线路跑向顺义公园,甲先跑一段路程后,乙开始出发,当乙超过甲150米时,乙停在此地等候甲,两人相遇后,乙和甲一起以甲原来的速度跑向顺义公园,如图是甲、乙两人在跑步的全过程中经过的路程y(米)与甲出发的时间x(秒)的函数图象,请根据题意解答下列问题.
(1)在跑步的全过程中,甲共跑了 米,甲的速度为 米/秒;
(2)求乙跑步的速度及乙在途中等候甲的时间;
(3)求乙出发多长时间第一次与甲相遇?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com