
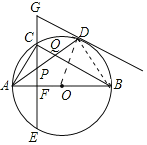
【题目】如图,在![]() 中,
中,![]() 是
是![]() 的直径,点
的直径,点![]() 是
是![]() 上一点,点
上一点,点![]() 是弧
是弧![]() 的中点,弦
的中点,弦![]() 于点
于点![]() ,过点
,过点![]() 的切线交
的切线交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,分别交
,分别交![]() 于点
于点![]() ,连接
,连接![]() .给出下列结论:①
.给出下列结论:①![]() ;②
;②![]() ;③点
;③点![]() 是
是![]() 的外心;④
的外心;④![]()
![]() .其中正确的是( )
.其中正确的是( )

A.①②③B.②③④C.①③④D.①②③④
【答案】B
【解析】
①由于![]() 与
与![]() 不一定相等,根据圆周角定理可判断①;
不一定相等,根据圆周角定理可判断①;
②连接OD,利用切线的性质,可得出∠GPD=∠GDP,利用等角对等边可得出GP=GD,可判断②;
③先由垂径定理得到A为![]() 的中点,再由C为
的中点,再由C为![]() 的中点,得到
的中点,得到![]() ,根据等弧所对的圆周角相等可得出∠CAP=∠ACP,利用等角对等边可得出AP=CP,又AB为直径得到∠ACQ为直角,由等角的余角相等可得出∠PCQ=∠PQC,得出CP=PQ,即P为直角三角形ACQ斜边上的中点,即为直角三角形ACQ的外心,可判断③;
,根据等弧所对的圆周角相等可得出∠CAP=∠ACP,利用等角对等边可得出AP=CP,又AB为直径得到∠ACQ为直角,由等角的余角相等可得出∠PCQ=∠PQC,得出CP=PQ,即P为直角三角形ACQ斜边上的中点,即为直角三角形ACQ的外心,可判断③;
④正确.证明△APF∽△ABD,可得AP×AD=AF×AB,证明△ACF∽△ABC,可得AC2=AF×AB,证明△CAQ∽△CBA,可得AC2=CQ×CB,由此即可判断④;
解:①错误,假设![]() ,则
,则![]() ,
,
![]()
![]() ,
,
![]()
![]() ,显然不可能,故①错误.
,显然不可能,故①错误.
②正确.连接![]() .
.
![]() 是切线,
是切线,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,故②正确.
,故②正确.
③正确.![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() 是直径,
是直径,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 点
点![]() 是
是![]() 的外心.故③正确.
的外心.故③正确.
④正确.连接![]() .
.
![]() ,
,![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
可得![]() ,
,
![]() ,
,![]() ,
,
![]() ,可得
,可得![]() ,
,
![]() .故④正确,
.故④正确,
故选:![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图像与坐标轴交于A、B两点,点C的坐标为
的图像与坐标轴交于A、B两点,点C的坐标为![]() ,二次函数
,二次函数![]() 的图像经过A、B、C三点.
的图像经过A、B、C三点.
(1)求二次函数的解析式
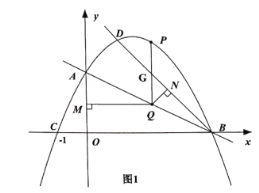
(2)如图1,已知点![]() 在抛物线上,作射线BD,点Q为线段AB上一点,过点Q作
在抛物线上,作射线BD,点Q为线段AB上一点,过点Q作![]() 轴于点M,作
轴于点M,作![]() 于点N,过Q作
于点N,过Q作![]() 轴交抛物线于点P,当QM与QN的积最大时,求点P的坐标;
轴交抛物线于点P,当QM与QN的积最大时,求点P的坐标;
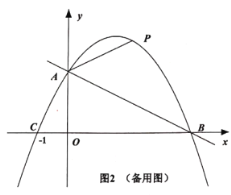
(3)在(2)的条件下,连接AP,若点E为抛物线上一点,且满足![]() ,求点E的坐标.
,求点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,公园中一正方形水池中有一喷泉,喷出的水流呈抛物线状,测得喷出口高出水面0.8m,水流在离喷出口的水平距离1.25m处达到最高,密集的水滴在水面上形成了一个半径为3m的圆,考虑到出水口过高影响美观,水滴落水形成的圆半径过大容易造成水滴外溅到池外,现决定通过降低出水口的高度,使落水形成的圆半径为2.75m,则应把出水口的高度调节为高出水面( )
A.0.55米B.![]() 米C.
米C.![]() 米D.0.4米
米D.0.4米
查看答案和解析>>
科目:初中数学 来源: 题型:
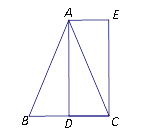
【题目】如图,在![]() 中,
中, ![]() ,
, ![]() 于点
于点![]() ,把线段
,把线段![]() 沿着
沿着![]() 的方向平移
的方向平移![]() 得到线段
得到线段![]() ,连接
,连接![]() .
.
问:(1)四边形![]() 是_________形;
是_________形;
(2)若![]() 的周长比
的周长比![]() 的周长大6,求四边形
的周长大6,求四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一次函数y1=kx+b的图象与反比例函数y2=![]() 的图象交于A(2,3),B(-3,n)两点.
的图象交于A(2,3),B(-3,n)两点.

(1)求一次函数和反比例函数的解析式;
(2)请直接写出,当x取何值时,y1>y2?
(3)若P是y轴上一点,且满足△PAB的面积是5,请直接写出OP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AC,BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=4,则下列结论:①![]() ;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )
;②S△BCE=36;③S△ABE=12;④△AEF~△ACD,其中一定正确的是( )

A. ①②③④ B. ①④ C. ②③④ D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
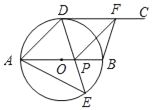
【题目】如图,AB为⊙O的直径,点D,E是位于AB两侧的半圆AB上的动点,射线DC切⊙O于点D.连接DE,AE,DE与AB交于点P,F是射线DC上一动点,连接FP,FB,且∠AED=45°.
(1)求证:CD∥AB;
(2)填空:
①若DF=AP,当∠DAE= 时,四边形ADFP是菱形;
②若BF⊥DF,当∠DAE= 时,四边形BFDP是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
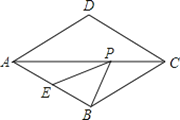
【题目】如图,菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值是( ).
A. 1 B. 2 C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com