练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    5．若关于的x方程x2+3x+a=0有一个根为-1，则a的值为（　　）
    A．-4B．-2C．2D．-4

    分析 根据一元二次方程的解的定义，把x=-1代入方程得到关于a的一次方程，然后解此一次方程即可．

    解答 解：把x=-1代入方程x2+3x+a=0得1-3+a=0，
    解得a=2．
    故选：C．

    点评 本题考查了一元二次方程的解：能使一元二次方程左右两边相等的未知数的值是一元二次方程的解．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    15．先化简，再求值
    （1）$\frac{{{x^2}-9}}{{{x^2}+6x+9}}•\frac{{3{x^3}+9{x^2}}}{{{x^2}-3x}}$，其中x=-$\frac{1}{3}$．
    （2）$\frac{x+y}{{{x^4}-{y^4}}}÷\frac{1}{{{x^2}+{y^2}}}$，其中x=8，y=11．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

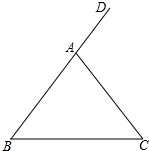    16．如图，△ABC中，AB=AC，∠DAC是△ABC的一个外角，
    实验与操作：
    根据要求进行尺规作图，并在图中标明相应的字母（保留作图痕迹，不写作法）
    （1）作∠DAC的平分线AM；
    （2）作线段AC的垂直平分线，与AM交于点F，与BC边交于点E，连接AE；
    （3）猜测AE和AF的关系，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    13．当n是正整数时，（2n+1）2-（2n-1）2（　　）
    A．等于4B．等于8C．等于4或-4D．是8的倍数

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．解下列不等式，并把它们的解集在数轴上表示出来：
    ①3x+1＞4x-1     
    ②5（x+3）-5≤10（x-1）
    ③$\frac{x}{3}$-$\frac{x-1}{2}$≤1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    10．如图，某校数学兴趣小组利用自制的直角三角形小硬纸板DEF来测量操场旗杆AB的高度，他们通过调整测量位置，使斜边DF与地面保持平行，并使边DE与旗杆顶点A在同一直线上，已知DE=0.5米，EF=0.25米，目测点D到地面的距离DG=1.5米，到旗杆的水平距离DC=20米，则旗杆的高度为11.5米．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．如图，△ABC中，AB=AC，以AB为直径的⊙O与BC相交于点D，与CA的延长线相交于点E，过点D作DF⊥AC于点F．
    （1）求证：DF是⊙O的切线；
    （2）若sinC=$\frac{\sqrt{3}}{3}$，半径OA=3，求AE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．列方程解应用题：

    为了丰富社会实践活动，引导学生科学探究，学校组织七年级同学走进中国科技馆，亲近科学，感受科技魅力．来到科技馆大厅，同学们就被大厅里会“跳舞”的“小球矩阵”吸引住了（如图1）．白色小球全部由计算机精准控制，每一只小球可以“悬浮”在大厅上空的不同位置，演绎着曲线、曲面、平面、文字和三维图案等各种动态造型．
    已知每个小球分别由独立的电机控制．图2，图3分别是9个小球可构成的两个造型，在每个造型中，相邻小球的高度差均为a．为了使小球从造型一（如图2）变到造型二（如图3），控制电机使造型一中的②，③，④，⑥，⑦，⑧号小球同时运动，②，③，④号小球向下运动，运动速度均为3米/秒；⑥，⑦，⑧号小球向上运动，运动速度均为2米/秒，当每个小球到达造型二的相应位置时就停止运动．已知⑦号小球比②号小球晚$\frac{4}{3}$秒到达相应位置，问②号小球运动了多少米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．德育处王主任将10份奖品分别放在10个完全相同的不透明礼盒中，准备将它们奖给小明等10位获“科技节活动先进个人”称号的同学．这些奖品中有5份是学习文具，3份是科普读物，2份是科技馆通票．小明同学从中随机取一份奖品，恰好取到科普读物的概率是（　　）
    A．$\frac{1}{2}$B．$\frac{3}{5}$C．$\frac{1}{5}$D．$\frac{3}{10}$

    查看答案和解析>>

    同步练习册答案