
【题目】在正方形![]() 中,点
中,点![]() 是
是![]() 边上一点,连接
边上一点,连接![]() .
.
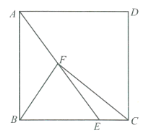

图1 图2
(1)如图1,点![]() 为
为![]() 的中点,连接
的中点,连接![]() .已知
.已知![]() ,
,![]() ,求
,求![]() 的长;
的长;
(2)如图2,过点![]() 作
作![]() 的垂线交
的垂线交![]() 于点
于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,点
,点![]() 为对角线
为对角线![]() 的中点,连接
的中点,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,求证:
,求证:![]() .
.
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)作![]() 于点
于点![]() ,由直角三角形斜边上的中线等于斜边的一半可推出
,由直角三角形斜边上的中线等于斜边的一半可推出![]() ,
,![]() ,在
,在![]() 中,利用三角函数求出BP,FP,在等腰三角形
中,利用三角函数求出BP,FP,在等腰三角形![]() 中,求出BE,再由勾股定理求出AB,进而得到BC和CP,再次利用勾股定理即可求出CF的长度.
中,求出BE,再由勾股定理求出AB,进而得到BC和CP,再次利用勾股定理即可求出CF的长度.
(2)过![]() 作
作![]() 垂直
垂直![]() 于点
于点![]() ,得矩形
,得矩形![]() ,首先证明
,首先证明![]() ,得
,得![]() ,再证明
,再证明![]() ,可推出得
,可推出得![]() .
.
解:(1)![]() 中,
中,![]() 为中线,
为中线,![]() ,
,
![]() ,
,![]() .
.
作![]() 于点
于点![]() ,如图,
,如图,
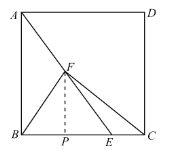
![]() 中,
中,![]()
![]()
在等腰三角形![]() 中,
中,
![]() ,
,
由勾股定理求得![]() ,
,
![]()
![]()
(2)过![]() 作
作![]() 垂直
垂直![]() 于点
于点![]() ,得矩形
,得矩形![]() ,
,
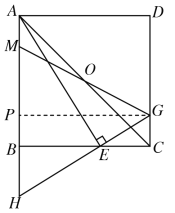
∵AB∥CD
∴∠MAO=∠GCO
在△AMO和△CGO中,
∵∠MAO=∠GCO,AO=CO,∠AOM=∠COG
∴△AMO≌△CGO(ASA)
∴AM=GC
∵四边形BCGP为矩形,
∴GC=PB,PG=BC=AB
∵AE⊥HG
∴∠H+∠BAE=90°
又∵∠AEB+∠BAE=90°
∴∠AEB=∠H
在△ABE和△GPH中,
∵∠AEB=∠H,∠ABE=∠GPH=90°,AB=PG
∴△ABE≌△GPH(AAS)
∴BE=PH
又∵CG=PB=AM
∴BE=PH=PB+BH=CG+BH=AM+BH
即AM+BH=BE.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线![]() 与y轴交于点A.
与y轴交于点A.
(1)直接写出点A的坐标;
(2)点A、B关于对称轴对称,求点B的坐标;
(3)已知点![]() ,
,![]() .若抛物线与线段PQ恰有两个公共点,结合函数图象,求a的取值范围.
.若抛物线与线段PQ恰有两个公共点,结合函数图象,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,反比例函数y= ![]() 的图象与一次函数y=x+b的图象交
的图象与一次函数y=x+b的图象交
于点A(1,4)、点B(-4,n).

(1)求一次函数和反比例函数的解析式;
(2)求△OAB的面积;
(3)直接写出一次函数值大于反比例函数值的自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学去年举办竞赛,颁发一二三等奖各若干名,获奖人数依次增加,各获奖学生获得的奖品价值依次减少(奖品单价都是整数元),其中有3人获得一等奖,每人获得的奖品价值34元,二等奖的奖品单价是5的倍数,获得三等奖的人数不超过10人,并且获得二三等奖的人数之和与二等奖奖品的单价相同.今年又举办了竞赛,获得一二三等奖的人数比去年分别增加了1人、2人、3人,购买对应奖品时发现单价分别上涨了6元、3元、2元.这样,今年购买奖品的总费用比去年增加了159元.那么去年购买奖品一共花了__________元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某养猪场对猪舍进行喷药消毒.在消毒的过程中,先经过![]() 的药物集中喷洒,再封闭猪舍
的药物集中喷洒,再封闭猪舍![]() ,然后再打开窗户进行通风.已知室内每立方米空气中含药量
,然后再打开窗户进行通风.已知室内每立方米空气中含药量![]() (
(![]() )与药物在空气中的持续时间
)与药物在空气中的持续时间![]() (
(![]() )之间的函数图象如图所示,其中在打开窗户通风前
)之间的函数图象如图所示,其中在打开窗户通风前![]() 与
与![]() 分别满足两个一次函数,在通风后
分别满足两个一次函数,在通风后![]() 与
与![]() 满足反比例函数.
满足反比例函数.
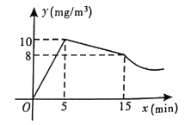
(1)求反比例函数的关系式;
(2)当猪舍内空气中含药量不低于![]() 且持续时间不少于
且持续时间不少于![]() ,才能有效杀死病毒,问此次消毒是否有效?
,才能有效杀死病毒,问此次消毒是否有效?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】兴发服装店老板用4500元购进一批某款T恤衫,由于深受顾客喜爱,很快售完,老板又用4950元购进第二批该款式T恤衫,所购数量与第一批相同,但每件进价比第一批多了9元.
(1)第一批该款式T恤衫每件进价是多少元?
(2)老板以每件120元的价格销售该款式T恤衫,当第二批T恤衫售出![]() 时,出现了滞销,于是决定降价促销,若要使第二批的销售利润不低于650元,剩余的T恤衫每件售价至少要多少元?(利润=售价﹣进价)
时,出现了滞销,于是决定降价促销,若要使第二批的销售利润不低于650元,剩余的T恤衫每件售价至少要多少元?(利润=售价﹣进价)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB⊥DE于A,C,O是AB上一点,且AC=CO=OB=2,以O为圆心作扇形BOF,F到直线AB的距离为![]() .
.
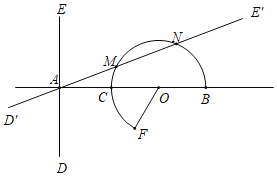
(1)求扇形BOF的面积:
(2)将直线DE绕A点旋转得到直线D'E';
①当直线D'E'与扇形BOF相切时,求旋转角的大小;
②设直线D'E'与扇形BOF的弧相交于M、N,若AM=MN,求MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某海滨浴场有100个遮阳伞,每个每天收费10元时,可全部租出,若每个每天提高2元,则减少10个伞租出,若每个每天收费再提高2元,则再减少10个伞租出,以此类推,为了投资少而获利大,每个遮阳伞每天应提高_______________。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com