
【题目】如图,点![]() 是正方形
是正方形![]() 边
边![]() .上一点,连接
.上一点,连接![]() ,作
,作![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)求证:![]() ;
;
(2)己知![]() ,四边形
,四边形![]() 的面积为
的面积为![]() ,求
,求![]() 的值.
的值.
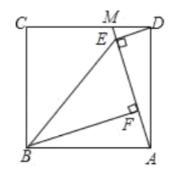
【答案】(1)见解析;(2)![]()
【解析】
(1)首先由正方形的性质得出BA=AD,∠BAD=90°,又由DE⊥AM于点E,BF⊥AM得出∠AFB=90°,∠DEA=90°,∠ABF=∠EAD,然后即可判定△ABF≌△DAE,即可得出BF=AE;
(2)首先设AE=x,则BF=x,DE=AF=2,然后将四边形的面积转化为两个三角形的面积之和,列出方程,得出BF,然后利用勾股定理得出BE,即可得解.
(1)证明:∵四边形ABCD为正方形,
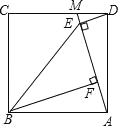
∴BA=AD,∠BAD=90°,
∵DE⊥AM于点E,BF⊥AM于点F,
∴∠AFB=90°,∠DEA=90°,
∵∠ABF+∠BAF=90°,∠EAD+∠BAF=90°,
∴∠ABF=∠EAD,
在△ABF和△DEA中
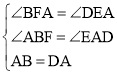 ,
,
∴△ABF≌△DAE(AAS),
∴BF=AE;
(2)设AE=x,则BF=x,DE=AF=2,
∵四边形ABED的面积为24,
∴![]() xx+
xx+![]() x2=24,
x2=24,
解得x1=6,x2=﹣8(舍去),
∴EF=x﹣2=4,
在Rt△BEF中,BE=![]() =2
=2![]() ,
,
∴![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,AB是定长线段,圆心O是AB的中点,AE、BF为切线,E、F为切点,满足AE=BF在![]() 上取动点G,过点G作切线交AE、BF的延长线于点D、C,当点G运动时,设AD=y,BC=x,则y与x所满足的函数关系式为( )
上取动点G,过点G作切线交AE、BF的延长线于点D、C,当点G运动时,设AD=y,BC=x,则y与x所满足的函数关系式为( )
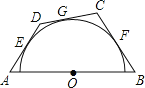
A.正比例函数y=kx(k为常数,k≠0,x>0)B.一次函数y=kx+b(k,b为常数,kb≠0,x>0)
C.二次函数y=ax2+bx+c(a,b,c为常数,a≠0,x>0)D.以上都不是
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形纸片ABCD,AB=9,BC=6,在矩形边上有一点P,且DP=3.将矩形纸片折叠,使点B与点P重合,折痕所在直线交矩形两边于点E,F,则EF长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+2ax+a2+3(其中x是自变量),当x≤﹣2时,y随x的增大而增大,且﹣2≤x≤1时,y的最大值为5,则a的值为( )
A.﹣1B.2C.﹣1或2D.![]() 或﹣
或﹣![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
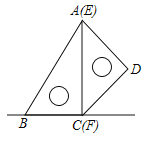
【题目】如图,一副含![]() 和
和![]() 角的三角板
角的三角板![]() 和
和![]() 拼合在一个平面上,边
拼合在一个平面上,边![]() 与
与![]() 重合,
重合,![]() .当点
.当点![]() 从点
从点![]() 出发沿
出发沿![]() 方向滑动时,点
方向滑动时,点![]() 同时从点
同时从点![]() 出发沿射线
出发沿射线![]() 方向滑动.当点
方向滑动.当点![]() 从点
从点![]() 滑动到点
滑动到点![]() 时,点
时,点![]() 运动的路径长为______
运动的路径长为______![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】质地均匀的骰子,6个面上分别标有数字1,2,3,4,5,6.同时抛掷这样的两枚骰子,落地后朝上的两个面上的数字之和为4的倍数的概率为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形![]() 中,点
中,点![]() 是
是![]() 边上一点,连接
边上一点,连接![]() .
.
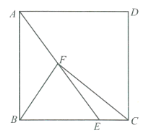

图1 图2
(1)如图1,点![]() 为
为![]() 的中点,连接
的中点,连接![]() .已知
.已知![]() ,
,![]() ,求
,求![]() 的长;
的长;
(2)如图2,过点![]() 作
作![]() 的垂线交
的垂线交![]() 于点
于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,点
,点![]() 为对角线
为对角线![]() 的中点,连接
的中点,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于题目“一段抛物线L:y=﹣x(x﹣3)+c(0≤x≤3)与直线l:y=x+2有唯一公共点,若c为整数,确定所有c的值,”甲的结果是c=1,乙的结果是c=3或4,则( )
A. 甲的结果正确
B. 乙的结果正确
C. 甲、乙的结果合在一起才正确
D. 甲、乙的结果合在一起也不正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:∠BAC.
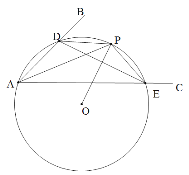
(1)如图,在平面内任取一点O;
(2)以点O为圆心,OA为半径作圆,交射线AB于点D,交射线AC于点E;
(3)连接DE,过点O作线段DE的垂线交⊙O于点P;
(4)连接AP,DP和PE.根据以上作图过程及所作图形,下列四个结论中:
①△ADE是⊙O的内接三角形; ② ![]() ;
;
③ DE=2PE; ④ AP平分∠BAC.
所有正确结论的序号是______________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com