
【题目】质地均匀的骰子,6个面上分别标有数字1,2,3,4,5,6.同时抛掷这样的两枚骰子,落地后朝上的两个面上的数字之和为4的倍数的概率为__________.
【答案】![]()
【解析】
采用列表法列举所有的可能性,找出数字和为4的倍数的情况数,再根据概率公式求解.
由题意,列表如下:
1 | 2 | 3 | 4 | 5 | 6 | |
1 | 1+1=2 | 1+2=3 | 1+3=4 | 1+4=5 | 1+5=6 | 1+6=7 |
2 | 2+1=3 | 2+2=4 | 2+3=5 | 2+4=6 | 2+5=7 | 2+6=8 |
3 | 3+1=4 | 3+2=5 | 3+3=6 | 3+4=7 | 3+5=8 | 3+6=9 |
4 | 4+1=5 | 4+2=6 | 4+3=7 | 4+4=8 | 4+5=9 | 4+6=10 |
5 | 5+1=6 | 5+2=7 | 5+3=8 | 5+4=9 | 5+5=10 | 5+6=11 |
6 | 6+1=7 | 6+2=8 | 6+3=9 | 6+4=10 | 6+5=11 | 6+6=12 |
总共的可能性由36种,其中和为4的倍数的情况有9种,
所以数字之和为4的倍数的概率P=![]() ,
,
故答案为![]() .
.


科目:初中数学 来源: 题型:
【题目】为满足市场需求,某超市在八月十五“中秋节”来临前夕,购进一种品牌的月饼,每盒进价40元,根据以往的销售经验发现:当售价定为每盒45元时,每天可以卖出700盒,每盒售价每提高1元,每天要少卖出20盒.
![]() 写出每天的销售量
写出每天的销售量![]() 盒
盒![]() 与每盒月饼上涨
与每盒月饼上涨![]() 元
元![]() 之间的函数关系式.
之间的函数关系式.
![]() 当每盒售价定为多少元时,当天的销售利润
当每盒售价定为多少元时,当天的销售利润![]() 元
元![]() 最大?最大利润是多少?
最大?最大利润是多少?
![]() 为稳定物价,有关管理部门限定,这种月饼每盒的利润不得高于进价的
为稳定物价,有关管理部门限定,这种月饼每盒的利润不得高于进价的![]() ,那么超市每天获得最大利润是多少?
,那么超市每天获得最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=x2+mx交x轴的负半轴于点A.点B是y轴正半轴上一点,点A关于点B的对称点A′恰好落在抛物线上.过点A′作x轴的平行线交抛物线于另一点C.若点A′的横坐标为1,则A′C的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个直径为2m的圆形铁皮,要从中剪出一个最大的圆心角为90°的扇形ABC.
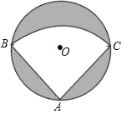
(1)求图中阴影部分的面积;
(2)若将扇形ABC围成一个圆锥,则该圆锥的底面半径最大是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】万州区某民营企业生产的甲、乙两种产品,已知2件甲商品的出厂总价与3件乙商品的出厂总价相同,3件甲商品的出厂总价比2件乙商品的出厂总价多150元.
(1)求甲、乙商品的出厂单价分别是多少元?
(2)为促进万州经济持续健康发展,为商家搭建展示平台,为行业创造交流机会,2019年万州区举办了多场商品展销会.外地一经销商计划购进甲商品200件,购进乙商品的数量是甲的4倍,恰逢展销会期间该企业正在对甲商品进行降价促销活动,甲商品的出厂单价降低了![]() ,该经销商购进甲的数量比原计划增加了
,该经销商购进甲的数量比原计划增加了![]() ,乙的出厂单价没有改变,该经销商购进乙的数量比原计划减少了
,乙的出厂单价没有改变,该经销商购进乙的数量比原计划减少了![]() ,结果该经销商付出的总货款与原计划的总货款恰好相同,求
,结果该经销商付出的总货款与原计划的总货款恰好相同,求![]() 的值
的值![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某养猪场对猪舍进行喷药消毒.在消毒的过程中,先经过![]() 的药物集中喷洒,再封闭猪舍
的药物集中喷洒,再封闭猪舍![]() ,然后再打开窗户进行通风.已知室内每立方米空气中含药量
,然后再打开窗户进行通风.已知室内每立方米空气中含药量![]() (
(![]() )与药物在空气中的持续时间
)与药物在空气中的持续时间![]() (
(![]() )之间的函数图象如图所示,其中在打开窗户通风前
)之间的函数图象如图所示,其中在打开窗户通风前![]() 与
与![]() 分别满足两个一次函数,在通风后
分别满足两个一次函数,在通风后![]() 与
与![]() 满足反比例函数.
满足反比例函数.
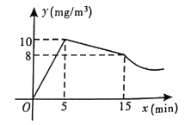
(1)求反比例函数的关系式;
(2)当猪舍内空气中含药量不低于![]() 且持续时间不少于
且持续时间不少于![]() ,才能有效杀死病毒,问此次消毒是否有效?
,才能有效杀死病毒,问此次消毒是否有效?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是矩形ABCD对角线AC上的一个动点(点E可以与点A和点C重合),连接BE.已知AB=3cm,BC=4cm.设A、E两点间的距离为xcm,BE的长度为ycm.
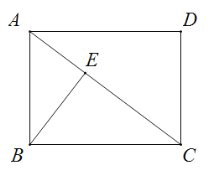
某同学根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行探究.
下面是该同学的探究过程,请补充完整:
(1)通过取点、画图、测量及分析,得到了x与y的几组值,如下表:

说明:补全表格时相关数值保留一位小数)
(2)建立平面直角坐标系,描出已补全后的表中各对对应值为坐标的点,画出该函数的图象.
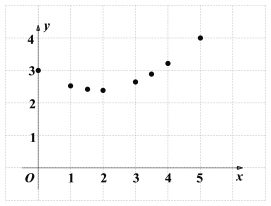
(3)结合画出的函数图象,解决问题:当BE=2AE时,AE的长度约为 cm.(结果保留一位小数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com