
【题目】有一个直径为2m的圆形铁皮,要从中剪出一个最大的圆心角为90°的扇形ABC.
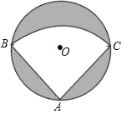
(1)求图中阴影部分的面积;
(2)若将扇形ABC围成一个圆锥,则该圆锥的底面半径最大是多少?
科目:初中数学 来源: 题型:
【题目】有两个可以自由转动的质地均匀转盘都被分成了3个全等的扇形,在每一扇形内均标有不同的自然数,如图所示,转动转盘,两个转盘停止后观察并记录两个指针所指扇形内的数字(若指针停在扇形的边线上,当作指向上边的扇形).
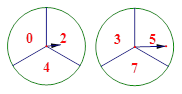
(1)用列表法或画树形图法求出同时转动两个转盘一次的所有可能结果;
(2)同时转动两个转盘一次,求“记录的两个数字之和为7”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,点M为二次函数y=x2+2bx+3c图象的顶点,一次函数y=kx﹣3(k>0)分别交x轴,y轴于点A,B.
(1)若b=1,c=1,判断顶点M是否在直线y=2x+1上,并说明理由;
(2)若该二次函数图象经过点C(1,﹣4),也经过点A,B,且满足kx﹣3<x2+2bx+3c,求该一次函数解析式,并直接写出自变量x的取值范围;
(3)设点P坐标为(m,n)在二次函数y=x2+2bx+3c上,当﹣2≤m≤2时,b﹣24≤n≤2b+4,试问:当b≥2或b≤﹣2时,对于该二次函数中任意的自变量x,函数值y是否始终大于﹣40?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+2ax+a2+3(其中x是自变量),当x≤﹣2时,y随x的增大而增大,且﹣2≤x≤1时,y的最大值为5,则a的值为( )
A.﹣1B.2C.﹣1或2D.![]() 或﹣
或﹣![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年,某贫困户的家庭年人均纯收入为2500元,通过政府产业扶持,发展了养殖业后,到2018年,家庭年人均纯收入达到了3600元.
(1)求该贫困户2016年到2018年家庭年人均纯收入的年平均增长率;
(2)若年平均增长率保持不变,2019年该贫困户的家庭年人均纯收入是否能达到4200元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】质地均匀的骰子,6个面上分别标有数字1,2,3,4,5,6.同时抛掷这样的两枚骰子,落地后朝上的两个面上的数字之和为4的倍数的概率为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明的家在某住宅楼AB的最顶层(AB⊥BC),他家的后面有一建筑物CD(CD∥AB),他很想知道这座建筑物的高度,于是在自家阳台的A处测得建筑物CD的底部C的俯角是43°,顶部D的仰角是25°,他又测得两建筑物之间的距离BC是28米,请你帮助小明求出建筑物CD的高度(精确到1米).
(参考数据:sin25°≈0.42,cos25°≈0.91,tan25°≈0.47;sin43°≈0.68,cos43°≈0.73,tan43°≈0.93.)

查看答案和解析>>
科目:初中数学 来源: 题型:
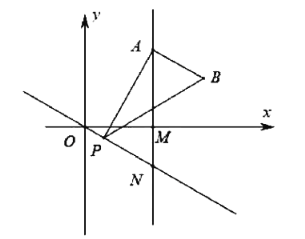
【题目】如图,已知点![]() 是第一象限内横坐标为2的一个定点,
是第一象限内横坐标为2的一个定点,![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() ,若点
,若点![]() 是线段
是线段![]() 上的一个动点,
上的一个动点,![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上运动时,
上运动时,![]() 点不变,
点不变,![]() 点随之运动,当点
点随之运动,当点![]() 从点
从点![]() 运动到点
运动到点![]() 时,则点
时,则点![]() 运动的路径长是( )
运动的路径长是( )
A.![]() B.
B.![]() C.2D.
C.2D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com