
����Ŀ����֪����MΪ���κ���y��x2+2bx+3cͼ��Ķ��㣬һ�κ���y��kx��3��k��0���ֱ�x�ᣬy���ڵ�A��B��
��1����b��1��c��1���ж϶���M�Ƿ���ֱ��y��2x+1�ϣ���˵�����ɣ�
��2�����ö��κ���ͼ����C��1����4����Ҳ������A��B��������kx��3��x2+2bx+3c�����һ�κ�������ʽ����ֱ��д���Ա���x��ȡֵ��Χ��
��3�����P����Ϊ��m��n���ڶ��κ���y��x2+2bx+3c�ϣ�����2��m��2ʱ��b��24��n��2b+4�����ʣ���b��2��b����2ʱ�����ڸö��κ�����������Ա���x������ֵy�Ƿ�ʼ�մ��ک�40����˵�����ɣ�
���𰸡���1��M����ֱ��y��2x+1�ϣ�����������2��y��x2��2x��3��x��3��x��0����3����b��2��b����2ʱ�����ڸö��κ�����������Ա���x������ֵyʼ�մ��ک�40
��������
(1)b��1,c��1ʱ,y��x2+2x+3,���M(��1,2),����M(��1,2)����y��2x+1��֤�Ƿ����㼴�ɣ�
(2)�����֪B(0,��3),C(1,��4),����y��x2+2bx+3c�õ�b����1,c����1,���A(![]() ,0),�ٽ���A������κ�������ʽ�õ�
,0),�ٽ���A������κ�������ʽ�õ�![]() ��
��![]() ��3��0,���k��1��
��3��0,���k��1��
(3)�����Գ���Ϊx����b,�ٵ���b����2ʱ,��b��2,��ʱb��24��4��4b+3c,��5b��3c��28,2b+4��4+4b+3c,��2b+3c��0,���y��x2+8x��8��(x+4)2��24����24����40���ڵ���b��2ʱ,��b����2,��ʱb��24��4+4b+3c,��3b+3c����28,2b+4��4��4b+3c,��6b��3c��0,���y��x2��![]() x��
x��![]() ��(x��
��(x��![]() )2��
)2��![]() ����
����![]() ����40��
����40��
�⣺(1)b��1,c��1ʱ,y��x2+2x+3=(x+1)2+2,
��M(��1,2),
����M(��1,2)����y��2x+1,��1��2,
��M������ֱ��y��2x+1�ϣ�
(2)��B��һ�κ���y=kx-3�ҽ���y��,��x=0,���y=-3,��B(0,-3).
��B(0,��3),C(1,��4),�������y��x2+2bx+3c.
����õ�:![]() ,���:b����1,c����1,
,���:b����1,c����1,
��y��x2��2x��3,
��A��y=kx-3����x��,��y=0,���x=![]() ,��A(
,��A(![]() ,0),
,0),
��![]() ��
��![]() ��3��0,
��3��0,
��k��1��k����3,
��k��0,
��k��1,
��y��x��3,
��x��3��x2��2x��3,
��x��3��x��0��
(3)�����Գ���Ϊx����b,
������b����2ʱ,��b��2,
��ʱb��24��4��4b+3c,��5b��3c��28,
2b+4��4+4b+3c,��2b+3c��0,
��b��4,c����![]() ,
,
��y��x2+8x��8��(x+4)2��24����24����40��
������b��2ʱ,��b����2,��ʱ
b��24��4+4b+3c,��3b+3c����28,
2b+4��4��4b+3c,��6b��3c��0,
��b����![]() ,c����
,c����![]() ,
,
��y��x2��![]() x��
x��![]() ��(x��
��(x��![]() )2��
)2��![]() ����
����![]() ����40��
����40��
����b��2��b����2ʱ,���ڸö��κ�����������Ա���x,����ֵyʼ�մ��ک�40��


 ȫ�ܲ����ĩС״Ԫϵ�д�
ȫ�ܲ����ĩС״Ԫϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
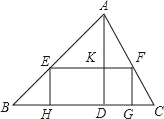
����Ŀ���������ABC�У���BC��Ϊ18����AD��Ϊ12
��1����ͼ������EFCH�ı�GH��BC���ϣ�������������E��F�ֱ���AB��AC���ϣ�EF��AD�ڵ�K����![]() ��ֵ��
��ֵ��
��2����EH��x������EFGH�����ΪS����S��x�ĺ�����ϵʽ������S�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ����40cm�Ľ�������������س�x��7cm����С�κ�y��9cm����С�Σ�ʣ�ಿ�������ϴ�������ʹ�������٣���������xӦΪ_��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У����κ���y��x2+bx+c��ͼ����x�ύ��A��B���㣬A����ԭ�����࣬B�������Ϊ��3��0������y�ύ�ڵ�C��0����3����
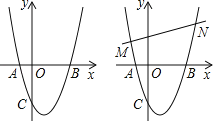
��1������κ�������ʽ��
��2������QΪ��������һ�㣬��S��ABQ��![]() S��ACQ�����Q�����ꣻ
S��ACQ�����Q�����ꣻ
��3����ֱ��l��y��mx+n������������������M��N��M��N����ߣ���PΪ��������һ���㣨����M��N�غϣ�����P��PHƽ����y�ύֱ��l�ڵ�H����![]() ��5����m��ֵ��
��5����m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y=x2+mx��x��ĸ������ڵ�A����B��y����������һ�㣬��A���ڵ�B�ĶԳƵ�A��ǡ�������������ϣ�����A����x���ƽ���߽�����������һ��C������A���ĺ�����Ϊ1����A��C�ij�Ϊ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������![]() ��
��![]() ��
��![]() ��
��![]() ���㣨
���㣨![]() ��
��![]() ����ࣩ����
����ࣩ����![]() ��
��![]() ����
����![]() �ύ��
�ύ��![]() �������ߵĶ�������Ϊ
�������ߵĶ�������Ϊ![]() .
.
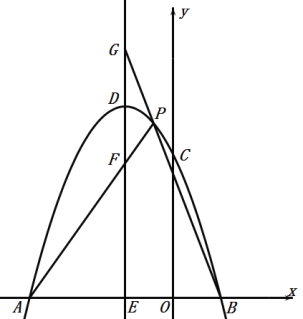
��1����![]() ��
��![]() ��������ꣻ
��������ꣻ
��2���������ߵĽ���ʽ��
��3������![]() ��ֱ��
��ֱ��![]() �ᣬ��
�ᣬ��![]() ���ڵ�
���ڵ�![]() ����
����![]() ����������
����������![]() ��
��![]() ������һ�����㣨��
������һ�����㣨��![]() ����
����![]() ��
��![]() �����غϣ���
�����غϣ���![]() ��
��![]() ��ֱ��
��ֱ��![]() �ֱ��ڵ�
�ֱ��ڵ�![]() ��
��![]() ������
������![]() �˶�ʱ��
�˶�ʱ��![]() �Ƿ�Ϊ��ֵ�����ǣ�������ö�ֵ�������ǣ���˵������.
�Ƿ�Ϊ��ֵ�����ǣ�������ö�ֵ�������ǣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ��ֱ��Ϊ2m��Բ����Ƥ��Ҫ���м���һ������Բ�Ľ�Ϊ90��������ABC��
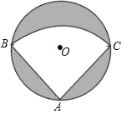
��1����ͼ����Ӱ���ֵ������
��2����������ABCΧ��һ��Բ�����Բ�ĵ���뾶����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ij��Ӫ��ҵ�����ļס������ֲ�Ʒ����֪2������Ʒ�ij����ܼ���3������Ʒ�ij����ܼ���ͬ��3������Ʒ�ij����ܼ۱�2������Ʒ�ij����ܼ۶�150Ԫ.
��1����ס�����Ʒ�ij������۷ֱ��Ƕ���Ԫ��
��2��Ϊ�ٽ����ݾ��ó���������չ��Ϊ�̼Ҵչʾƽ̨��Ϊ��ҵ���콻�����ᣬ2019���������ٰ��˶ೡ��Ʒչ����.���һ�����̼ƻ���������Ʒ200������������Ʒ�������Ǽ�4����ǡ��չ�����ڼ����ҵ���ڶԼ���Ʒ���н��۴����������Ʒ�ij������۽�����![]() ���þ����̹�����������ԭ�ƻ�������
���þ����̹�����������ԭ�ƻ�������![]() ���ҵij�������û�иı䣬�þ����̹����ҵ�������ԭ�ƻ�������
���ҵij�������û�иı䣬�þ����̹����ҵ�������ԭ�ƻ�������![]() ������þ����̸������ܻ�����ԭ�ƻ����ܻ���ǡ����ͬ����
������þ����̸������ܻ�����ԭ�ƻ����ܻ���ǡ����ͬ����![]() ��ֵ
��ֵ![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���ڵȱ�������ABC�У�CDΪ���ߣ���Q���߶�CD���˶������߶�QA�Ƶ�Q˳ʱ����ת��ʹ�õ�A�Ķ�Ӧ��E��������BC�ϣ�����BQ�����DAQ=��
��0�㣼����60��������30�㣩.
��1����0�㣼����30��ʱ��
����ͼ1�������⻭��ͼ�Σ������BQE���ú�����ʽ�ӱ�ʾ����
��̽���߶�CE��AC��CQ֮���������ϵ��������֤����
��2����30�㣼����60��ʱ��ֱ��д���߶�CE��AC��CQ֮���������ϵ.


![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com