
【题目】如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于点C(0,﹣3).
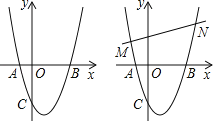
(1)求二次函数解析式;
(2)若点Q为抛物线上一点,且S△ABQ=![]() S△ACQ,求点Q的坐标;
S△ACQ,求点Q的坐标;
(3)若直线l:y=mx+n与抛物线有两个交点M,N(M在N的左边),P为抛物线上一动点(不与M,N重合).过P作PH平行于y轴交直线l于点H,若![]() =5,求m的值.
=5,求m的值.
【答案】(1)y=x2﹣2x﹣3;(2)点Q的坐标为(![]() ,﹣
,﹣![]() )或(
)或(![]() ,
,![]() );(3)m=±2.
);(3)m=±2.
【解析】
(1)抛物线与y轴交于点C(0,-3),则c=-3,将点B的坐标代入抛物线表达式并解得:b=-2,即可求解;
(2)分点Q在x轴下方、点Q在x轴上方两种情况,分别求解即可;
(3)MH=![]() (t-x1),同理:NH=(x2-t)
(t-x1),同理:NH=(x2-t)![]() ,MHMN=(m2+1)(mt+n-t2+2t+3)=(m2+1)PH,即可求解.
,MHMN=(m2+1)(mt+n-t2+2t+3)=(m2+1)PH,即可求解.
解:(1)抛物线与y轴交于点C(0,﹣3),则c=﹣3,
将点B的坐标代入抛物线表达式并解得:b=﹣2,
故抛物线的表达式为:y=x2﹣2x﹣3;
(2)设:点Q(m,m2﹣2m﹣3),
①当点Q在x轴下方时,如图1,
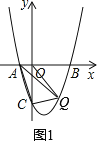
S△ACQ=![]() ×4×(﹣m2+2m+3),
×4×(﹣m2+2m+3),
S△ABQ=S△AOC+S△QOC﹣S△AOQ=![]() ﹣
﹣![]() ×3×m﹣
×3×m﹣![]() ×1×(﹣m2+2m+3)=
×1×(﹣m2+2m+3)=![]() m2+
m2+![]() m,
m,
则:![]() ×4×(﹣m2+2m+3)=
×4×(﹣m2+2m+3)=![]() m2+
m2+![]() m,
m,
解得:m=![]() 或﹣1(舍去﹣1),故点P(
或﹣1(舍去﹣1),故点P(,﹣
![]() );
);
②当点Q在x轴上方时,如图2,
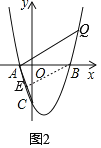
取AC的中点E(﹣![]() ,﹣
,﹣![]() ),
),
S△ABQ=![]() S△ACQ,则点E、B到AQ的距离相等,BE∥AQ,
S△ACQ,则点E、B到AQ的距离相等,BE∥AQ,
直线BE的表达式中的k值为:![]() ,
,
同理直线BQ的表达式为:y=![]() x+
x+![]() ,
,
∴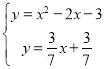 ,
,
解得:x=![]() 或﹣1(舍去﹣1),
或﹣1(舍去﹣1),
故点Q(![]() ,
,![]() );
);
综上,点Q的坐标为:(![]() ,﹣
,﹣![]() )或(
)或(![]() ,
,![]() );
);
(3)过点H作x轴的平行线RH,过点M、N分别作RH的垂线交于点R、S,
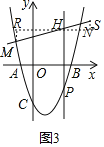
设点M、N的横坐标分别为x1,x2,点P(t,t2﹣2t﹣3),则点H(m,mt+n),
则PH=mt+n﹣t2+2t+3,
联立直线与抛物线的表达式并整理得:
x2﹣(m+2)x﹣3﹣n=0,
则x1+x2=m+2,x1x2=﹣3﹣n
直线M、N的k值为m,即tan∠RHM=m=tanα,则cosα=![]() ,
,
∴MH=![]() (t﹣x1),同理:NH=(x2﹣t)
(t﹣x1),同理:NH=(x2﹣t)![]() ,
,
∴MHMN=(m2+1)(mt+n﹣t2+2t+3)=(m2+1)PH,
而![]() ,则m2+1=5,
,则m2+1=5,
解得:m=±2.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线y=x2﹣4x+n(x>0)的图象记为G1,将G1绕坐标原点旋转180°得到图象G2,图象G1和G2合起来记为图象G.
(1)若点P(﹣1,2)在图象G上,求n的值.
(2)当n=﹣1时.
①若Q(t,1)在图象G上,求t的值.
②当k≤x≤3(k<3)时,图象G对应函数的最大值为5,最小值为﹣5,直接写出k的取值范围.
(3)当以A(﹣3,3)、B(﹣3,﹣1)、C(2,﹣1)、D(2,3)为顶点的矩形ABCD的边与图象G有且只有三个公共点时,直接写出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是![]() 上一动点,连接AP,作∠APC=45°,交弦AB于点C.AB=6cm.
上一动点,连接AP,作∠APC=45°,交弦AB于点C.AB=6cm.
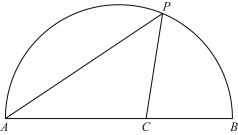
小元根据学习函数的经验,分别对线段AP,PC,AC的长度进行了测量.
下面是小元的探究过程,请补充完整:
(1)下表是点P是![]() 上的不同位置,画图、测量,得到线段AP,PC,AC长度的几组值,如下表:
上的不同位置,画图、测量,得到线段AP,PC,AC长度的几组值,如下表:
AP/cm | 0 | 1.00 | 2.00 | 3.00 | 4.00 | 5.00 | 6.00 |
PC/cm | 0 | 1.21 | 2.09 | 2.69 | m | 2.82 | 0 |
AC/cm | 0 | 0.87 | 1.57 | 2.20 | 2.83 | 3.61 | 6.00 |
①经测量m的值是 (保留一位小数).
②在AP,PC,AC的长度这三个量中,确定![]() 的长度是自变量,
的长度是自变量,![]() 的长度和 的长度都是这个自变量的函数;
的长度和 的长度都是这个自变量的函数;
(2)在同一平面直角坐标系xOy中,画出(1)中所确定的函数图象;

(3)结合函数图象,解决问题:当△ACP为等腰三角形时,AP的长度约为 cm(保留一位小数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司根据市场需求销售A、B两种型号的净水器,每台A型净水器比每台B型净水器进价多200元,用5万元购进A型净水器与用4.5万元购进B型净水器的数量相等.
(1)求每台A型、B型净水器的进价各是多少元?
(2)该公司计划用不超过9.8万元购进A,B两种型号的净水器共50台,其中A型、B型净水器每台售价分别为2500元、2180元,设A型净水器为x台.
①求x的取值范围.
②若公司决定从销售A型净水器的利润中每台捐献a(100<a<150)元给贫困村饮水改造爱心工程,求售完这50台净水器后获得的最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有两个可以自由转动的质地均匀转盘都被分成了3个全等的扇形,在每一扇形内均标有不同的自然数,如图所示,转动转盘,两个转盘停止后观察并记录两个指针所指扇形内的数字(若指针停在扇形的边线上,当作指向上边的扇形).
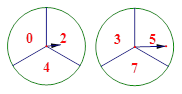
(1)用列表法或画树形图法求出同时转动两个转盘一次的所有可能结果;
(2)同时转动两个转盘一次,求“记录的两个数字之和为7”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:t1,t2是方程t2+2t﹣24=0的两个实数根,且t1<t2,抛物线y=![]() x2+bx+c的图象经过点A(t1,0),B(0,t2).
x2+bx+c的图象经过点A(t1,0),B(0,t2).
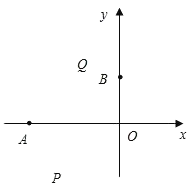
(1)求这个抛物线的解析式;
(2)设点P(x,y)是抛物线上一动点,且位于第三象限,四边形OPAQ是以OA为对角线的平行四边形,求平行四边形OPAQ的面积S与x之间的函数关系式,并写出自变量x的取值范围;
(3)在(2)的条件下,当平行四边形OPAQ的面积为24时,是否存在这样的点P,使OPAQ为正方形?若存在,求出P点坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,点M为二次函数y=x2+2bx+3c图象的顶点,一次函数y=kx﹣3(k>0)分别交x轴,y轴于点A,B.
(1)若b=1,c=1,判断顶点M是否在直线y=2x+1上,并说明理由;
(2)若该二次函数图象经过点C(1,﹣4),也经过点A,B,且满足kx﹣3<x2+2bx+3c,求该一次函数解析式,并直接写出自变量x的取值范围;
(3)设点P坐标为(m,n)在二次函数y=x2+2bx+3c上,当﹣2≤m≤2时,b﹣24≤n≤2b+4,试问:当b≥2或b≤﹣2时,对于该二次函数中任意的自变量x,函数值y是否始终大于﹣40?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年,某贫困户的家庭年人均纯收入为2500元,通过政府产业扶持,发展了养殖业后,到2018年,家庭年人均纯收入达到了3600元.
(1)求该贫困户2016年到2018年家庭年人均纯收入的年平均增长率;
(2)若年平均增长率保持不变,2019年该贫困户的家庭年人均纯收入是否能达到4200元?
查看答案和解析>>
科目:初中数学 来源: 题型:
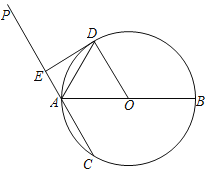
【题目】如图,AB是⊙O的直径,过点A的直线PC交⊙O于A,C两点,AD平分∠PAB,射线AD交⊙O于点D,过点D作DE⊥PA于点E.
(1)求证:ED为⊙O的切线;
(2)若AB=10,ED=2AE,求AC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com