
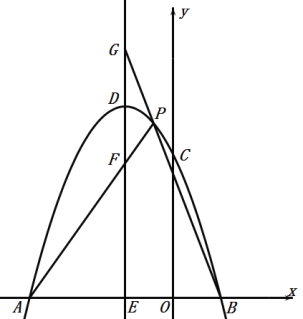
【题目】如图,在平面直角坐标系中,抛物线![]() 交
交![]() 轴
轴![]() 、
、![]() 两点(
两点(![]() 在
在![]() 的左侧),且
的左侧),且![]() ,
,![]() ,与
,与![]() 轴交于
轴交于![]() ,抛物线的顶点坐标为
,抛物线的顶点坐标为![]() .
.
(1)求![]() 、
、![]() 两点的坐标;
两点的坐标;
(2)求抛物线的解析式;
(3)过点![]() 作直线
作直线![]() 轴,交
轴,交![]() 轴于点
轴于点![]() ,点
,点![]() 是抛物线上
是抛物线上![]() 、
、![]() 两点间的一个动点(点
两点间的一个动点(点![]() 不与
不与![]() 、
、![]() 两点重合),
两点重合),![]() 、
、![]() 与直线
与直线![]() 分别交于点
分别交于点![]() 、
、![]() ,当点
,当点![]() 运动时,
运动时,![]() 是否为定值?若是,试求出该定值;若不是,请说明理由.
是否为定值?若是,试求出该定值;若不是,请说明理由.
科目:初中数学 来源: 题型:
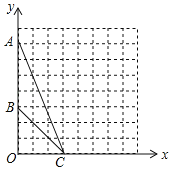
【题目】如图,在平面直角坐标系xOy中,点A的坐标为(0,7),点B的坐标为(0,3),点C的坐标为(3,0).
(1)在图中作出△ABC的外接圆(利用格图确定圆心);
(2)圆心坐标为 ;外接圆半径r为 ;
(2)若在x轴的正半轴上有一点D,且∠ADB=∠ACB,则点D的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司根据市场需求销售A、B两种型号的净水器,每台A型净水器比每台B型净水器进价多200元,用5万元购进A型净水器与用4.5万元购进B型净水器的数量相等.
(1)求每台A型、B型净水器的进价各是多少元?
(2)该公司计划用不超过9.8万元购进A,B两种型号的净水器共50台,其中A型、B型净水器每台售价分别为2500元、2180元,设A型净水器为x台.
①求x的取值范围.
②若公司决定从销售A型净水器的利润中每台捐献a(100<a<150)元给贫困村饮水改造爱心工程,求售完这50台净水器后获得的最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
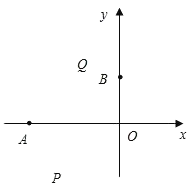
【题目】已知:t1,t2是方程t2+2t﹣24=0的两个实数根,且t1<t2,抛物线y=![]() x2+bx+c的图象经过点A(t1,0),B(0,t2).
x2+bx+c的图象经过点A(t1,0),B(0,t2).
(1)求这个抛物线的解析式;
(2)设点P(x,y)是抛物线上一动点,且位于第三象限,四边形OPAQ是以OA为对角线的平行四边形,求平行四边形OPAQ的面积S与x之间的函数关系式,并写出自变量x的取值范围;
(3)在(2)的条件下,当平行四边形OPAQ的面积为24时,是否存在这样的点P,使OPAQ为正方形?若存在,求出P点坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,点M为二次函数y=x2+2bx+3c图象的顶点,一次函数y=kx﹣3(k>0)分别交x轴,y轴于点A,B.
(1)若b=1,c=1,判断顶点M是否在直线y=2x+1上,并说明理由;
(2)若该二次函数图象经过点C(1,﹣4),也经过点A,B,且满足kx﹣3<x2+2bx+3c,求该一次函数解析式,并直接写出自变量x的取值范围;
(3)设点P坐标为(m,n)在二次函数y=x2+2bx+3c上,当﹣2≤m≤2时,b﹣24≤n≤2b+4,试问:当b≥2或b≤﹣2时,对于该二次函数中任意的自变量x,函数值y是否始终大于﹣40?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
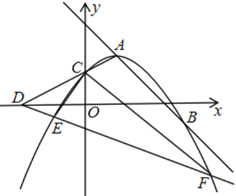
【题目】如图,抛物线y=![]() x2+mx+m(m>0)的顶点为A,交y轴于点C.
x2+mx+m(m>0)的顶点为A,交y轴于点C.
(1)求出点A的坐标(用含m的式子表示);
(2)若直线y=﹣x+n经过点A,与抛物线交于另一点B,证明:AB的长是定值;
(3)连接AC,延长AC交x轴于点D,作直线AD关于x轴对称的直线,与抛物线分别交于E、F两点.若∠ECF=90°,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年,某贫困户的家庭年人均纯收入为2500元,通过政府产业扶持,发展了养殖业后,到2018年,家庭年人均纯收入达到了3600元.
(1)求该贫困户2016年到2018年家庭年人均纯收入的年平均增长率;
(2)若年平均增长率保持不变,2019年该贫困户的家庭年人均纯收入是否能达到4200元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】校园内有一个由两个全等的六边形(边长为![]() )围成的花坛,现将这个花坛在原有的基础上扩建成如图所示的一个菱形区域,并在新扩建的部分种上草坪,则扩建后菱形区域的周长为( )
)围成的花坛,现将这个花坛在原有的基础上扩建成如图所示的一个菱形区域,并在新扩建的部分种上草坪,则扩建后菱形区域的周长为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
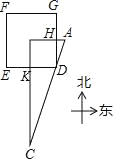
【题目】《九章算术》是中国传统数学最重要的著作,在“勾股”章中有这样一个问题:“今有邑方二百步,各中开门,出东门十五步有木,问:出南门几步面见木?”用今天的话说,大意是:如图,DEFG是一座边长为200步(“步”是古代的长度单位)的正方形小城,东门H位于GD的中点,南门K位于ED的中点,出东门15步的A处有一树木,求出南门多少步恰好看到位于A处的树木(即点D在直线AC上)?请你计算KC的长为多少步.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com