
【题目】一根长40cm的金属棒,欲将其截成x根7cm长的小段和y根9cm长的小段,剩余部分作废料处理.若使废料最少,则正整数x应为_.
 精英口算卡系列答案
精英口算卡系列答案科目:初中数学 来源: 题型:
【题目】如图,点P是![]() 上一动点,连接AP,作∠APC=45°,交弦AB于点C.AB=6cm.
上一动点,连接AP,作∠APC=45°,交弦AB于点C.AB=6cm.
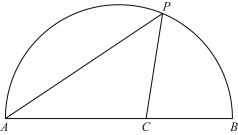
小元根据学习函数的经验,分别对线段AP,PC,AC的长度进行了测量.
下面是小元的探究过程,请补充完整:
(1)下表是点P是![]() 上的不同位置,画图、测量,得到线段AP,PC,AC长度的几组值,如下表:
上的不同位置,画图、测量,得到线段AP,PC,AC长度的几组值,如下表:
AP/cm | 0 | 1.00 | 2.00 | 3.00 | 4.00 | 5.00 | 6.00 |
PC/cm | 0 | 1.21 | 2.09 | 2.69 | m | 2.82 | 0 |
AC/cm | 0 | 0.87 | 1.57 | 2.20 | 2.83 | 3.61 | 6.00 |
①经测量m的值是 (保留一位小数).
②在AP,PC,AC的长度这三个量中,确定![]() 的长度是自变量,
的长度是自变量,![]() 的长度和 的长度都是这个自变量的函数;
的长度和 的长度都是这个自变量的函数;
(2)在同一平面直角坐标系xOy中,画出(1)中所确定的函数图象;

(3)结合函数图象,解决问题:当△ACP为等腰三角形时,AP的长度约为 cm(保留一位小数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将等边△ABC绕点C顺时针旋转90得到△DEC,∠ACD的平分线CF交DE于点F,连接AE,AF.
(1)求∠CEA度数;
(2)求证AF⊥CE.
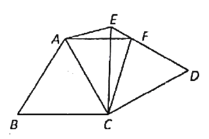
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司根据市场需求销售A、B两种型号的净水器,每台A型净水器比每台B型净水器进价多200元,用5万元购进A型净水器与用4.5万元购进B型净水器的数量相等.
(1)求每台A型、B型净水器的进价各是多少元?
(2)该公司计划用不超过9.8万元购进A,B两种型号的净水器共50台,其中A型、B型净水器每台售价分别为2500元、2180元,设A型净水器为x台.
①求x的取值范围.
②若公司决定从销售A型净水器的利润中每台捐献a(100<a<150)元给贫困村饮水改造爱心工程,求售完这50台净水器后获得的最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有两个可以自由转动的质地均匀转盘都被分成了3个全等的扇形,在每一扇形内均标有不同的自然数,如图所示,转动转盘,两个转盘停止后观察并记录两个指针所指扇形内的数字(若指针停在扇形的边线上,当作指向上边的扇形).
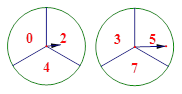
(1)用列表法或画树形图法求出同时转动两个转盘一次的所有可能结果;
(2)同时转动两个转盘一次,求“记录的两个数字之和为7”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,点M为二次函数y=x2+2bx+3c图象的顶点,一次函数y=kx﹣3(k>0)分别交x轴,y轴于点A,B.
(1)若b=1,c=1,判断顶点M是否在直线y=2x+1上,并说明理由;
(2)若该二次函数图象经过点C(1,﹣4),也经过点A,B,且满足kx﹣3<x2+2bx+3c,求该一次函数解析式,并直接写出自变量x的取值范围;
(3)设点P坐标为(m,n)在二次函数y=x2+2bx+3c上,当﹣2≤m≤2时,b﹣24≤n≤2b+4,试问:当b≥2或b≤﹣2时,对于该二次函数中任意的自变量x,函数值y是否始终大于﹣40?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明的家在某住宅楼AB的最顶层(AB⊥BC),他家的后面有一建筑物CD(CD∥AB),他很想知道这座建筑物的高度,于是在自家阳台的A处测得建筑物CD的底部C的俯角是43°,顶部D的仰角是25°,他又测得两建筑物之间的距离BC是28米,请你帮助小明求出建筑物CD的高度(精确到1米).
(参考数据:sin25°≈0.42,cos25°≈0.91,tan25°≈0.47;sin43°≈0.68,cos43°≈0.73,tan43°≈0.93.)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com