
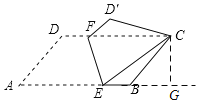
【题目】如图,将ABCD沿EF对折,使点A落在点C处,若∠A=60°,AD=4,AB=8,则AE的长为__.

【答案】![]()
【解析】
过点C作CG⊥AB的延长线于点G,易证△D′CF≌△ECB(ASA),从而可知D′F=EB,CF=CE,设AE=x,在△CEG中,利用勾股定理列出方程即可求出x的值.
过点C作CG⊥AB的延长线于点G,
在ABCD中,∠D=∠EBC,AD=BC,∠A=∠DCB,
由于ABCD沿EF对折,
∴∠D′=∠D=∠EBC,∠D′CE=∠A=∠DCB,
D′C=AD=BC,
∴∠D′CF+∠FCE=∠FCE+∠ECB,
∴∠D′CF=∠ECB,且∠D'=∠EBC,D'C=BC
∴△D′CF≌△ECB(ASA)
∴D′F=EB,CF=CE,
∵DF=D′F,
∴DF=EB,AE=CF
设AE=x,则EB=8﹣x,CF=x,
∵BC=4,∠CBG=60°,
∴BG=![]() BC=2,
BC=2,
在Rt△BCG中,由勾股定理可知:CG=![]() ,
,
∴EG=EB+BG=8﹣x+2=10﹣x
在Rt△CEG中,由勾股定理可知:(10﹣x)2+(2![]() )2=x2,
)2=x2,
∴x=![]()
∴AE=![]()
故答案为:![]()


 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案科目:初中数学 来源: 题型:
【题目】 小明遇到这样一个问题
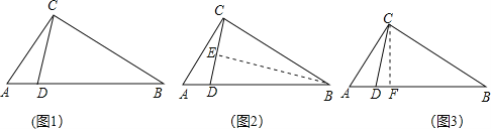
如图1,△ABC中,∠ACB=90°,点D在AB上,且BD=BC,求证:∠ABC=2∠ACD.
小明发现,除了直接用角度计算的方法外,还可以用下面两种方法:
方法2:如图2,作BE⊥CD,垂足为点E.
方法3:如图3,作CF⊥AB,垂足为点F.
根据阅读材料,从三种方法中任选一种方法,证明∠ABC=2∠ACD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次篮球比赛中,如图队员甲正在投篮.已知球出手时离地面![]() m,与篮圈中心的水平距离为7 m,球出手后水平距离为4 m时达到最大高度4 m,设篮球运行轨迹为抛物线,篮圈距地面3 m.
m,与篮圈中心的水平距离为7 m,球出手后水平距离为4 m时达到最大高度4 m,设篮球运行轨迹为抛物线,篮圈距地面3 m.
(1)建立如图所示的平面直角坐标系,问此球能否准确投中?
(2)此时,对方队员乙在甲面前1 m处跳起盖帽拦截,已知乙的最大摸高为3.1 m,那么他能否获得成功?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.阜阳市某家快递公司,2017年3月份与5月份完成投递的快递总件数分别为10万件和12.1万件.现假定该公司每月投递的快递总件数的增长率相同.
(1)求该快递公司投递快递总件数的月平均增长率?
(2) 如果平均每人每月最多可投递快递0.6万件,那么该公司现有的21名快递投递业务员能否完成2017年6月份的快递投递任务?如果不能,请问至少需要增加几名业务员?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实验探究:
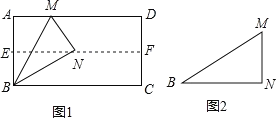
(1)如图1,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展开;再一次折叠纸片,使点A落在EF上,并使折痕经过点B,得到折痕BM,同时得到线段BN,MN.请你观察图1,猜想∠MBN的度数是多少,并证明你的结论.
(2)将图1中的三角形纸片BMN剪下,如图2,折叠该纸片,探究MN与BM的数量关系,写出折叠方案,并结合方案证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,O为坐标原点,A(1,1),在x轴上确定点P,使△AOP为等腰三角形,则符合条件的点P的个数共有( )
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)解方程x2﹣4x=12;
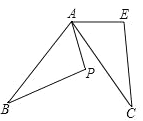
(2)如图,△ABP是由△ACE绕A点旋转得到的,若∠APB=110°,∠B=30°,∠PAC=20°,求旋转角的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com