
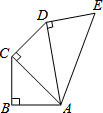
 如图所示,AB=BC=CD=DE=1,AB⊥BC,AC⊥CD,AD⊥DE,则五边形ABCDE的面积等于( )
如图所示,AB=BC=CD=DE=1,AB⊥BC,AC⊥CD,AD⊥DE,则五边形ABCDE的面积等于( )| A. | $\frac{3}{2}$ | B. | $\frac{3}{2}$$\sqrt{2}$ | C. | $\frac{3}{2}$$\sqrt{3}$ | D. | $\frac{1+\sqrt{2}+\sqrt{3}}{2}$ |
分析 根据勾股定理求出AC和AD的长,分别求出每个三角形的面积,相加即可得出答案.
解答 解:在Rt△ABC中,由勾股定理得:AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,
在Rt△ACD中,CD=1,AC=$\sqrt{2}$,由勾股定理得:AD=$\sqrt{A{C}^{2}+C{D}^{2}}$=$\sqrt{3}$,
所以五边形ABCDE的面积为S=S△ABC+S△ACD+S△ADE=$\frac{1}{2}×1×1$+$\frac{1}{2}×\sqrt{2}$×1+$\frac{1}{2}×\sqrt{3}$×1=$\frac{1+\sqrt{2}+\sqrt{3}}{2}$,
故选D.
点评 本题考查了勾股定理和三角形的面积的应用,解此题的关键是能根据勾股定理求出AC和AD的长,难度适中.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:填空题
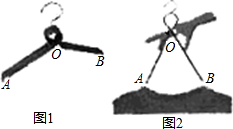 由于木质衣架没有柔性,在挂置衣服的时候不太方便操作.小敏设计了一种衣架,在使用时能轻易收拢,然后套进衣服后松开即可.如图1,衣架杆OA=OB=18cm,若衣架收拢时,∠AOB=60°,如图2,则此时A,B两点之间的距离是18cm.
由于木质衣架没有柔性,在挂置衣服的时候不太方便操作.小敏设计了一种衣架,在使用时能轻易收拢,然后套进衣服后松开即可.如图1,衣架杆OA=OB=18cm,若衣架收拢时,∠AOB=60°,如图2,则此时A,B两点之间的距离是18cm.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
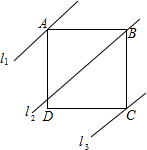 如图,四边形ABCD是正方形,直线l1、l2、l3分别通过A、B、C三点,且l1∥l2∥l3,若l1与l2的距离为6,l2与l3的距离为8,则正方形ABCD的面积等于100.
如图,四边形ABCD是正方形,直线l1、l2、l3分别通过A、B、C三点,且l1∥l2∥l3,若l1与l2的距离为6,l2与l3的距离为8,则正方形ABCD的面积等于100.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com