
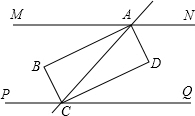
 已知MN∥PQ,AB,BC分别平分∠MAC,∠PCA,交于点B,AD,DC分别平分∠NAC,∠QCA,交于点D.求证:四边形ABCD是矩形.
已知MN∥PQ,AB,BC分别平分∠MAC,∠PCA,交于点B,AD,DC分别平分∠NAC,∠QCA,交于点D.求证:四边形ABCD是矩形.| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
 证明:∵AB、BC分别平分∠MAC、∠PCA,
证明:∵AB、BC分别平分∠MAC、∠PCA,| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:
 如图,在△ABC中,AB=AC,D、E是△ABC内两点,AD平分∠BAC,∠EBC=∠E=60°,且BE=8cm.
如图,在△ABC中,AB=AC,D、E是△ABC内两点,AD平分∠BAC,∠EBC=∠E=60°,且BE=8cm.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知∠1=∠2,∠B=∠C,小丽在图上把两组相等角的信息标注出来后,略加分析,便发现CE∥BF.同桌的小聪说:“我还能得到∠A=∠D呢.”小丽深入思考后,很快也明白了小聪是怎么得到∠A=∠D的了.你能写出得到CE∥BF,∠A=∠D的过程吗?
如图,已知∠1=∠2,∠B=∠C,小丽在图上把两组相等角的信息标注出来后,略加分析,便发现CE∥BF.同桌的小聪说:“我还能得到∠A=∠D呢.”小丽深入思考后,很快也明白了小聪是怎么得到∠A=∠D的了.你能写出得到CE∥BF,∠A=∠D的过程吗?查看答案和解析>>
科目:初中数学 来源: 题型:
| A、近似数4.50和4.5是不一样的 |
| B、近似数6.0精确到十分位 |
| C、近似数7.3万精确到千位 |
| D、近似数2.30×105精确到百分位 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com