
 如图,抛物线
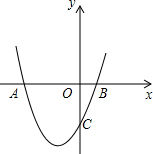
如图,抛物线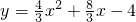 与x轴交于点A、B,与y轴交于点C.
与x轴交于点A、B,与y轴交于点C.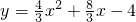 ,
, x2+
x2+ x-4=0,
x-4=0,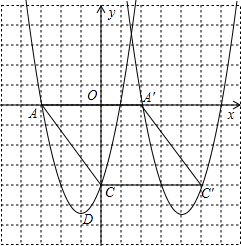 ∵x=0时,y=-4,
∵x=0时,y=-4, x2+
x2+ x-4=
x-4= (x2+2x)-4=
(x2+2x)-4= (x+1)2-
(x+1)2- ,
, );
);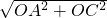 =
= =5,
=5, (x+1)2-
(x+1)2- 向右平移5个单位长度得到平移后抛物线的表达式为y=
向右平移5个单位长度得到平移后抛物线的表达式为y= (x-4)2-
(x-4)2- ;
;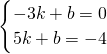 ,解得
,解得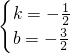 ,
, x-
x- ,
, ×(-1)-
×(-1)- =-1,
=-1,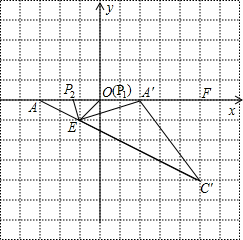 ∴A′E=
∴A′E=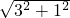 =
= ,A′C′=AA′=5,C′E=
,A′C′=AA′=5,C′E=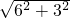 =3
=3 ,AE=
,AE= =
= .
.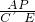 =
=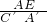 时,△AEP∽△C′A′E,或者当
时,△AEP∽△C′A′E,或者当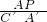 =
=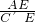 时,△AEP∽△C′EA′,
时,△AEP∽△C′EA′,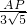 =
= ,或者
,或者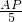 =
=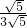 ,
, ,
, ,0);
,0); ,∠C′A′F=
,∠C′A′F= ,
, ,0).
,0).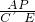 =
=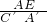 时,△AEP∽△C′A′E,或者当
时,△AEP∽△C′A′E,或者当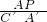 =
=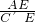 时,△AEP∽△C′EA′,分别将数据代入计算即可求出AP的值,进而得到P点坐标为;②如果点P在A点左边的x轴上;先由∠EAP>90°,∠EA′C′>90°,得出以点A、E、P为顶点的三角形与△A′C′E相似时,A与A′一定对应,再证明∠EAP≠∠EA′C′,得出△AEP与△A′C′E不可能相似.
时,△AEP∽△C′EA′,分别将数据代入计算即可求出AP的值,进而得到P点坐标为;②如果点P在A点左边的x轴上;先由∠EAP>90°,∠EA′C′>90°,得出以点A、E、P为顶点的三角形与△A′C′E相似时,A与A′一定对应,再证明∠EAP≠∠EA′C′,得出△AEP与△A′C′E不可能相似.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
 如图,抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,-3),设抛物线的顶点为D.
如图,抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,-3),设抛物线的顶点为D.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,抛物线与x轴交于A(x1,0)、B(x2,0)两点,且x1<x2,与y轴交于点C(0,-4),其中x1,x2是方程x2-4x-12=0的两个根.
如图,抛物线与x轴交于A(x1,0)、B(x2,0)两点,且x1<x2,与y轴交于点C(0,-4),其中x1,x2是方程x2-4x-12=0的两个根.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•历下区一模)如图,抛物线与x轴交于A(-1,0),B(4,0)两点,与y轴交于C(0,3),M是抛物线对称轴上的任意一点,则△AMC的周长最小值是
(2012•历下区一模)如图,抛物线与x轴交于A(-1,0),B(4,0)两点,与y轴交于C(0,3),M是抛物线对称轴上的任意一点,则△AMC的周长最小值是| 10 |
| 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,抛物线与y轴交于点A(0,4),与x轴交于B、C两点.其中OB、OC是方程的x2-10x+16=0两根,且OB<OC.
如图,抛物线与y轴交于点A(0,4),与x轴交于B、C两点.其中OB、OC是方程的x2-10x+16=0两根,且OB<OC.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,抛物线与x轴交于A、B(6,0)两点,且对称轴为直线x=2,与y轴交于点C(0,-4).
如图,抛物线与x轴交于A、B(6,0)两点,且对称轴为直线x=2,与y轴交于点C(0,-4).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com