
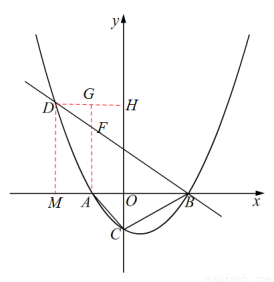
如图,已知抛物线 (
( 为常数,且
为常数,且 )与
)与 轴从左至右依次交于A,B两点,与
轴从左至右依次交于A,B两点,与 轴交于点C,经过点B的直线
轴交于点C,经过点B的直线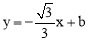 与抛物线的另一交点为D.
与抛物线的另一交点为D.
(1)若点D的横坐标为-5,求抛物线的函数表达式;
(2)若在第一象限的抛物线上有点P,使得以A,B,P为顶点的三角形与△ABC相似,求 的值;
的值;
(3)在(1)的条件下,设F为线段BD上一点(不含端点),连接AF,一动点M从点A出发,沿线段AF以每秒1个单位的速度运动到F,再沿线段FD以每秒2个单位的速度运动到D后停止. 当点F的坐标是多少时,点M在整个运动过程中用时最少?

(1)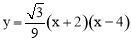 ;(2)
;(2)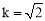 或
或 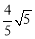 ;(3)F
;(3)F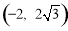 .
.
【解析】
试题分析:(1)根据点在曲线上点的坐标满足方程的关系,依次求出 的值得到直线的解析式、点D的纵坐标、
的值得到直线的解析式、点D的纵坐标、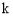 的值得到抛物线的函数表达式.
的值得到抛物线的函数表达式.
∵BM=9,AB=6,∴BF=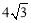 ,BD=
,BD=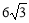 ,AF=
,AF=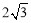
(2)分△PAB∽△ABC和△PAB∽△BAC两种情况讨论即可.
(3)过点D作DH⊥y轴于点H,过点A作AG⊥DH于点G,交BD于点F,则点F即为所求,理由是,由于点M在线段AF上以每秒1个单位的速度运动,在线段FD上以每秒2个单位的速度运动,从而根据直线BD的倾斜角是30°知道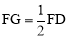 ,又根据垂直线段最短的性质知点F即为所求,从而根据含30°直角三角形的性质求解即可.
,又根据垂直线段最短的性质知点F即为所求,从而根据含30°直角三角形的性质求解即可.
试题解析:(1)∵抛物线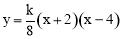 (
(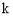 为常数,且
为常数,且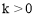 )与
)与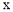 轴从左至右依次交于A,B两点,
轴从左至右依次交于A,B两点,
∴A(-2,0),B(4,0).
∵点B在直线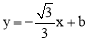 上,∴
上,∴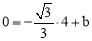 ,即
,即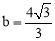 .
.
∴直线的解析式为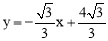 .
.
∵点D在直线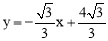 上,且横坐标为-5,∴纵坐标为
上,且横坐标为-5,∴纵坐标为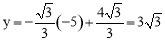 .
.
∵点D在抛物线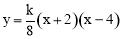 上,∴
上,∴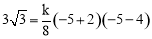 ,解得
,解得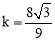 .
.
∴抛物线的函数表达式为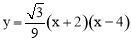 .
.
(2)易得,点C的坐标为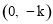 ,则
,则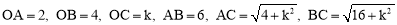 .
.
设点P的坐标为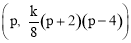 ,
,
分两种情况:
①若△PAB∽△ABC,则∠PAB=∠ABC,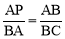 .
.
∴由∠PAB=∠ABC 得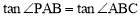 ,即
,即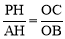 .
.
∴ ,解得
,解得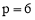 .
.
此时点P的坐标为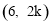 ,
,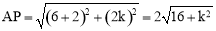 ,
,
∴由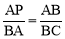 得
得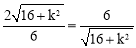 ,解得
,解得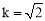 .
.
②若△PAB∽△BAC,则∠PAB=∠BAC,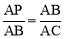 .
.
∴由∠PAB=∠BAC 得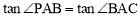 ,即
,即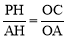 .
.
∴ ,解得
,解得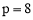 .
.
此时点P的坐标为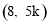 ,
,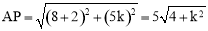 ,
,
∴由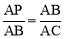 得
得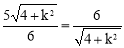 ,解得
,解得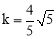 .
.
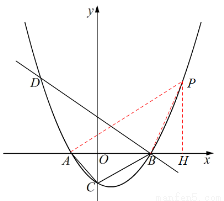
(3)如图,过点D作DH⊥y轴于点H,过点A作AG⊥DH于点G,交BD于点F,则点F即为所求.
∵直线BD的解析式为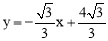 ,∴∠FBA=∠FGD=30°.
,∴∠FBA=∠FGD=30°.
∵AB=6,∴AF=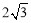 .
.
∴点F的坐标为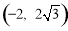 .
.
考点:1.单动点问题;2.二次函数和一次函数交点问题;3.曲线上点的坐标与方程的关系;4.勾股定理;5.相似三角形的判定;6.垂直线段最短的性质;7.分类思想和数形结合思想的应用.


科目:初中数学 来源:2014年初中毕业升学考试(四川资阳卷)数学(解析版) 题型:填空题
如图,以O(0,0)、A(2,0)为顶点作正△OAP1,以点P1和线段P1A的中点B为顶点作正△P1BP2,再以点P2和线段P2B的中点C为顶点作△P2CP3,…,如此继续下去,则第六个正三角形中,不在第五个正三角形上的顶点P6的坐标是 .

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川甘孜卷)数学(解析版) 题型:填空题
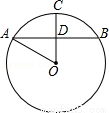
如图,点A,B,C在圆O上,OC⊥AB,垂足为D,若⊙O的半径是10cm,AB=12cm,则CD= cm.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川甘孜卷)数学(解析版) 题型:选择题
如图,一个简单几何体的三视图的主视图与左视图都为正三角形,其俯视图为正方形,则这个几何体是( )
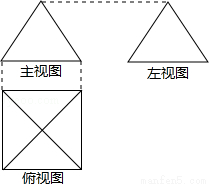
A.四棱锥 B.正方体 C.四棱柱 D.三棱锥
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川成都卷)数学(解析版) 题型:填空题
在边长为1的小正方形组成的方格纸中,称小正方形的顶点为“格点”,顶点全在格点上的多边形为“格点多边形”.格点多边形的面积记为S,其内部的格点数记为N,边界上的格点数记为L,例如,图中的三角形ABC是格点三角形,其中S=2,N=0,L=6;图中格点多边形DEFGHI所对应的S,N,L分别是 _.经探究发现,任意格点多边形的面积S可表示为S=aN+bL+c,其中a,b,c为常数,则当N=5,L=14时,S= .(用数值作答)

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川德阳卷)数学(解析版) 题型:解答题
为落实国家“三农”政策,某地政府组织40辆汽车装运A、B、C三种农产品共200吨到外地销售,按计划,40辆车都要装运,每辆车只能装运同一种农产品,且必须装满,根据下表提供的信息,解答下列问题:
农产品种类 A B C
每辆汽车的装载量(吨) 4 5 6
(1)如果装运C种农产品需13辆汽车,那么装运A、B两种农产品各需多少辆汽车?
(2)如果装运每种农产品至少需要11辆汽车,那么车辆的装运方案有几种?写出每种装运方案.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(四川宜宾卷)数学(解析版) 题型:选择题
若关于x的一元二次方程的两个根为x1=1,x2=2,则这个方程是( )
A.x2+3x﹣2=0 B.x2﹣3x+2=0 C.x2﹣2x+3=0 D.x2+3x+2=0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com