
【题目】如图,在△ABC中,∠B=90°,BC=8 AB=6cm,动点P从点A开始沿边AB向点B以1cm/s的速度移动,动点Q从点B开始沿边BC向点C以2cm/s的速度移动.若P,Q两点分别从A,B两点同时出发,在运动过程中,△PBQ的最大面积是( )
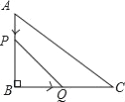
A. 18cm2 B. 12cm2 C. 9cm2 D. 3cm2
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案科目:初中数学 来源: 题型:
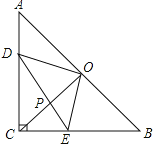
【题目】如图,在等腰直角△ABC中,∠ACB=90°,CO⊥AB于点O,点D、E分别在边AC、BC上,且AD=CE,连结DE交CO于点P,给出以下结论:
①△DOE是等腰直角三角形;②∠CDE=∠COE;③若AC=1,则四边形CEOD的面积为![]() ;④
;④![]() ,其中所有正确结论的序号是 .
,其中所有正确结论的序号是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我省教育厅下发了《在全省中小学幼儿园广泛深入开展节约教育》的通知,通知中要求各学校全面持续开展“光盘行动”.某市教育局督导检查组为了调查学生对“节约教育”内容的了解程度(程度分为:“A—了解很多”,“B—了解较多”,“C—了解较少”,“D—不了解”),对本市一所中学的学生进行了抽样调查,我们将这次调查的结果绘制成以下两幅统计图.
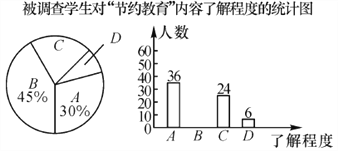
根据以上信息,解答下列问题:
(1)本次抽样调查了多少名学生?
(2)补全两幅统计图;
(3)若该中学共有1 800名学生,请你估计这所中学的所有学生中,对“节约教育”内容“了解较多”的有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用配方法解关于x的一元二次方程x2﹣2x﹣3=0,配方后的方程可以是( )
A. (x﹣1)2=4 B. (x+1)2=4 C. (x﹣1)2=16 D. (x+1)2=16
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com