
【题目】如图,在□ABCD中,点E在AD上,以BE为折痕将△ABE翻折,点A恰好落在CD边上的点F处. 已知△EDF的周长为12,△BCF的周长为22,求CF的长.

 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案科目:初中数学 来源: 题型:
【题目】对于一次函数y=-2x+4,下列结论错误的是( )
A. 函数的图象与x轴的交点坐标是![]()
B. 函数值随自变量的增大而减小
C. 函数的图象不经过第三象限
D. 函数的图象向下平移4个单位长度得![]() 的图象
的图象
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1+∠2=180°,∠3=∠B,试说明DE∥BC.下面是部分推导过程,请你在括号内填上推导依据或内容:
证明:∵∠1+∠2=180°(已知)
∠1=∠4 ( )
∴∠2+∠4=180°(等量代换)
∵EH∥AB( )
∴∠B= ( )
∵∠3=∠B(已知)
∴∠3=∠EHC(等量代换)
∴DE∥BC ( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列两个等式:![]() ,
,![]() ,给出定义如下:我们称使等式
,给出定义如下:我们称使等式 ![]() 成立的一对有理数
成立的一对有理数![]() ,
,![]() 为“共生有理数对”,记为(
为“共生有理数对”,记为(![]() ,
,![]() ),如:数对(
),如:数对(![]() ,
,![]() ),(
),(![]() ,
,![]() ),都是“共生有理数对”.
),都是“共生有理数对”.
(1)数对(![]() ,
,![]() ),(
),(![]() ,
,![]() )中是“共生有理数对”吗?说明理由.
)中是“共生有理数对”吗?说明理由.
(2)若(![]() ,
,![]() )是“共生有理数对”,则(
)是“共生有理数对”,则(![]() ,
,![]() )是“共生有理数对”吗?说明理由.
)是“共生有理数对”吗?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年中考前,张老师为了解全市初三男生体育考试项目的选择情况(每人限选一项),在全市范围内随机调查了部分初三男生,将调查结果分成五类:A.推实心球(2kg);B.立定跳远;C.半场运球;D.跳绳;E.其他,并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题: 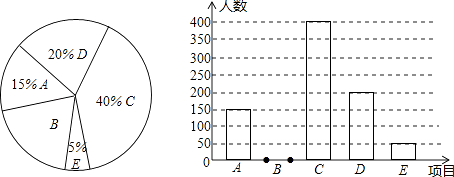
(1)将上面的条形统计图补充完整;
(2)假定全市初三毕业学生中有32000名男生,试估计全市初三男生中选半场运球的人数有多少人;
(3)甲、乙两名初三男生在上述选择率较高的三个项目:B.立定跳远;C.半场运球;D.跳绳中各选一项,同时选择半场运球、立定跳远的概率是多少?请用列表法或画树形图的方法加以说明并列出所有等可能的结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两位探险者到沙漠进行探险,没有了水,需要寻找水源.为了不致于走散,他们用两部对话机联系,已知对话机的有效距离为15千米.早晨8:00甲先出发,他以6千米/时的速度向东行走,1小时后乙出发,他以5千米/时的速度向北行进,上午10:00,甲、乙二人相距多远?还能保持联系吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新冠肺炎疫情爆发以来,口罩成为需求最为迫切的防护物资.在这个关键时刻,我国某企业利用自身优势转产口罩,这背后不仅体现出企业强烈的社会责任感,更是我国人民团结一心抗击疫情的决心.据悉该企业3月份的口罩日产能已达到500万只,预计今后数月内都将保持同样的产能,则3月份(按31天计算)该企业生产的口罩总数量用科学记数法表示为( )
A.![]() 只B.
只B.![]() 只C.
只C.![]() 只D.
只D.![]() 只
只
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠CAB=70°,将△ABC绕点A按逆时针方向旋转一个锐角α到△AB′C′的位置,连接CC′,若CC′∥AB,则旋转角α的度数为( )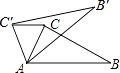
A.40°
B.50°
C.30°
D.35°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com