
【题目】对于下列结论:①二次函数y=6x2,当x>0时,y随x的增大而增大;②关于x的方程a(x+m)2+b=0的解是x1=﹣2,x2=1(a、m、b均为常数,a≠0),则方程a(x+m+2)2+b=0的解是x1=﹣4,x2=﹣1;③设二次函数y=x2+bx+c,当x≤1时,总有y≥0,当1≤x≤3时,总有y≤0,那么c的取值范围是c≥3.其中,正确结论的个数是( )
A. 0个 B. 1个 C. 2个 D. 3个
【答案】D
【解析】
①根据二次函数的性质即可得出抛物线y=6x2的对称轴为y轴,结合a=6>0即可得出当x>0时,y随x的增大而增大,结论①正确;
②将x=﹣2和1代入一元二次方程可得出x+m的值,再令x+m+2=该数值可求出x值,从而得出结论②正确;
③由“当x≤1时,总有y≥0,当1≤x≤3时,总有y≤0”可得出当x=1时y=0且抛物线的对称轴≥2,解不等式即可得出b≤﹣4、c≥3,结论③正确.综上即可得出结论.
∵在二次函数y=6x2中,a=6>0,b=0,
∴抛物线的对称轴为y轴,当x>0时,y随x的增大而增大,
∴①结论正确;
∵关于x的方程a(x+m)2+b=0的解是x1=-2,x2=1,
∴x+m=-2+m或1+m,
∴方程a(x+m+2)2+b=0中,
x+m+2=-2+m或x+m+2=1+m,
解得:x1=-4,x2=-1,
∴②结论正确;
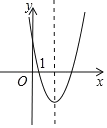
∵二次函数y=x2+bx+c,当x≤1时,总有y≥0,当1≤x≤3时,总有y≤0,
∴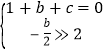
解得:b≤-4,c≥3,
∴结论③正确.
故选D


科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线AC,BD相交于点O,过点O作OE⊥AC交AB于E,若BC=4,△AOE的面积为5,则sin∠BOE的值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径CD垂直于弦AB,垂足为E,F为DC延长线上一点,且∠CBF=∠CDB.
(1)求证:FB为⊙O的切线;
(2)若AB=8,CE=2,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的对角线AC,BD相交于点O,延长CB至点F,使CF=CA,连接AF,∠ACF的平分线分别交AF,AB,BD于点E,N,M,连接EO.
(1)已知EO=![]() ,求正方形ABCD的边长;
,求正方形ABCD的边长;
(2)猜想线段EM与CN的数量关系并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
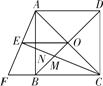
【题目】已知⊙O的直径为10,点A,点B,点C在⊙O上,∠CAB的平分线交⊙O于点D.
(Ⅰ)如图①,若BC为⊙O的直径,AB=6,求AC,BD,CD的长;
(Ⅱ)如图②,若∠CAB=60°,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场有A,B两种商品,若买2件A商品和1件B商品,共需80元;若买3件A商品和2件B商品,共需135元.
(1)设A,B两种商品每件售价分别为a元、b元,求a、b的值;
(2)B商品每件的成本是20元,根据市场调查:若按(1)中求出的单价销售,该商场每天销售B商品100件;若销售单价每上涨1元,B商品每天的销售量就减少5件.
①求每天B商品的销售利润y(元)与销售单价(x)元之间的函数关系?
②求销售单价为多少元时,B商品每天的销售利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线的对称轴是x=1,与x轴有两个交点,与y轴的交点坐标是(0,3),把它向下平移2个单位长度后,得到新的抛物线的解析式是y=ax2+bx+c,以下四个结论:
①b2﹣4ac<0,②abc<0,③4a+2b+c=1,④a﹣b+c>0中,其中正确的是_____(填序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个拱形桥架可以近似看作是由等腰梯形ABD8D1和其上方的抛物线D1OD8组成.若建立如图所示的直角坐标系,跨度AB=44米,∠A=45°,AC1=4米,点D2的坐标为(-13,-1.69),则桥架的拱高OH=________米.

查看答案和解析>>
科目:初中数学 来源: 题型:
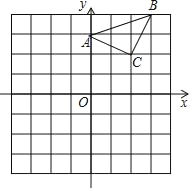
【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)画出△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是 ;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com