
在矩形ABCD中,将点A翻折到对角线BD上的点M处,折痕BE交AD于
点E.将点C翻折到对角线BD上的点N处,折痕DF交BC于点F.
(1)求证:四边形BFDE为平行四边形;
(2)若四边形BFDE为菱形,且AB=2,求BC的长.
 |
(1)证明:∵四边形ABCD是矩形,
∴∠A=∠C=90°,AB=CD,AB∥CD,
∴∠ABD=∠CDB,
∵在矩形ABCD中,将点A翻折到对角线BD上的点M处,折痕BE交AD于点E.将点C翻折到对角线BD上的点N处,
∴∠ABE=∠EBD=∠ABD,∠CDF=∠CDB,
∴∠ABE=∠CDF,
在△ABE和△CDF中
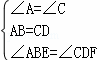 ,
,
∴△ABE≌△CDF(ASA),
∴AE=CF,
∵四边形ABCD是矩形,
∴AD=BC,AD∥BC,
∴DE=BF,DE∥BF,
∴四边形BFDE为平行四边形;
解法二:证明:∵四边形ABCD是矩形,
∴∠A=∠C=90°,AB=CD,AB∥CD,
∴∠ABD=∠CDB,
∴∠EBD=∠FDB,
∴EB∥DF,
∵ED∥BF,
∴四边形BFDE为平行四边形.
(2)解:∵四边形BFDE为菱形,
∴BE=ED,∠EBD=∠FBD=∠ABE,
∵四边形ABCD是矩形,
∴AD=BC,∠ABC=90°,
∴∠ABE=30°,
∵∠A=90°,AB=2,
∴AE=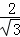 =
=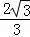 ,BE=2AE=
,BE=2AE=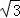 ,
,
∴BC=AD=AE+ED=AE+BE=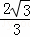 +
+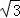 =2
=2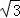 .
.


科目:初中数学 来源: 题型:
一次数学测试,某小组五名同学的成绩统计如下表所示,求m,n的值.
| 组员 | 甲 | 乙 | 丙 | 丁 | 戊 | 方差 | 平均成绩 |
| 得分 | 81 | 79 | m | 80 | 82 | n | 80 |
查看答案和解析>>
科目:初中数学 来源: 题型:
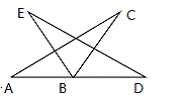
如图,△ABC绕点B顺时针旋转到△EBD位置,若∠A=30°,∠D=15°,A,B,D在同一直线上,则旋转的角度是()
A. 50° B . 45° C. 40° D. 30°
查看答案和解析>>
科目:初中数学 来源: 题型:
将抛物线y=2x2-4x-5向上平移6个单位长度,再向左平移2个单位长度,最后所得抛物线绕原点转180°,得到新的抛物线解析式()
A.y=2x2-4x-5 B.y=-2x2+4x-1 C. y=2x2+12x+19 D. y=-2x2-12x-17
查看答案和解析>>
科目:初中数学 来源: 题型:
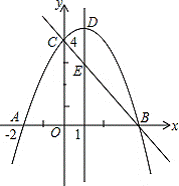
抛物线y=ax2+bx+c(a≠0)与y轴于点C(0,4),与x轴交于点A、B,其中A(-2,0),抛物线对称轴直线x=1与抛物线交于点D,与直线BC交于点E
(1)求抛物线的解析式及其顶点坐标
(2)若点F事BC上方的抛物线上的一个动点,是否存在点F,使四边形ABFC的面积为17,若存在求出F点坐标。不存在说明理由。
(3)平行于DE的一条动直线l与BC相交于点P,与抛物线相交于点Q,若以D、E、P、Q为顶点的四边形是平行四边形,求P坐标。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com