
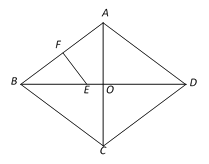
【题目】如图,点O是菱形ABCD对角线的交点,点E在BO上,EF垂直平分AB,垂足为F.
(1)求证:△BEF ∽△DCO;
(2)若AB=10,AC=12,求线段EF的长.
科目:初中数学 来源: 题型:
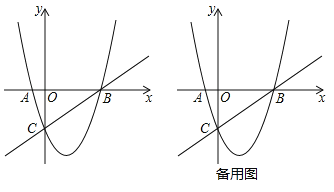
【题目】如图,直线![]() 与x轴交于点
与x轴交于点![]() 与y轴交于点C,抛物线
与y轴交于点C,抛物线![]() 经过点B,C,与x轴的另一个交点为A.
经过点B,C,与x轴的另一个交点为A.
(1)求抛物线的解析式;
(2)点P是直线![]() 下方抛物线上一动点,求四边形
下方抛物线上一动点,求四边形![]() 面积最大时点P的坐标;
面积最大时点P的坐标;
(3)若M是抛物线上一点,且![]() ,请直接写出点M的坐标.
,请直接写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为积极响应政府提出的“绿色发展·低碳出行”号召,某社区决定购置一批共享单车,经市场调查得知,购买3量男式单车与4辆女式单车费用相同,购买5辆男式单车与4辆女式单车共需16000元.
(1)求男式单车和女式单车的单价;
(2)该社区要求男式单比女式单车多4辆,两种单车至少需要22辆,购置两种单车的费用不超过50000元,该社区有几种购置方案?怎样购置才能使所需总费用最低,最低费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,l是经过A(2,0),B(0,b)两点的直线,且b0,点C的坐标为(2,0),当点B移动时,过点C作CD⊥l交于点D.
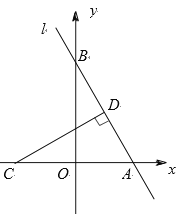
(1)求点D,O之间的距离;
(2)当tan∠CDO=![]() 时,求直线l的解析式;
时,求直线l的解析式;
(3)在(2)的条件下,直接写出△ACD与△AOB重叠部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合,若BC=3,则折痕CE的长为( )
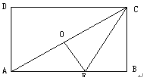
A. ![]() B.
B. ![]() C.
C. ![]() D. 6
D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,设抛物线y=ax2+bx+c与x轴交于两个不同的点A(﹣1,0),B(m,0),与y轴交于点C(0,﹣2),且∠ACB=90度.
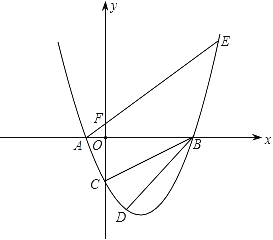
(1)求m的值和抛物线的解析式;
(2)已知点D(1,n)在抛物线上,过点A的直线y=x+1交抛物线于另一点E,求点D和点E的坐标;
(3)在x轴上是否存在点P,使以点P,B,D为顶点的三角形与三角形AEB相似?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校与图书馆在同一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达目的地.两人之间的距离y(米)与时间t(分钟)之间的函数关系如图所示.乙回到学校用了______分钟.
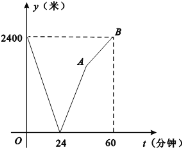
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,与x轴负半轴交于B,与正半轴交于点
,与x轴负半轴交于B,与正半轴交于点![]() ,且
,且![]() .
.
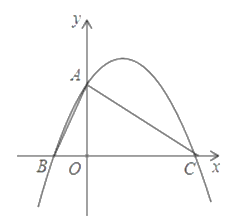
(1)求该二次函数解析式;
(2)若![]() 是线段
是线段![]() 上一动点,作
上一动点,作![]() ,交
,交![]() 于点
于点![]() ,连结
,连结![]() 当
当![]() 面积最大时,求点
面积最大时,求点![]() 的坐标;
的坐标;
(3)若点![]() 为
为![]() 轴上方的抛物线上的一个动点,连接
轴上方的抛物线上的一个动点,连接![]() ,设所得
,设所得![]() 的面积为
的面积为![]() .问:是否存在一个
.问:是否存在一个![]() 的值,使得相应的点
的值,使得相应的点![]() 有且只有
有且只有![]() 个,若有,求出这个
个,若有,求出这个![]() 的值,并求此时点
的值,并求此时点![]() 的横坐标;若不存在,请说明理由.
的横坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com