
【题目】如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为( )

A. 130°B. 120°C. 110°D. 100°
【答案】B
【解析】
根据要使△AMN的周长最小,即利用点的对称,让三角形的三边在同一直线上,作出A关于BC和ED的对称点A′,A″,即可得出∠AA′M+∠A″=∠HAA′=60°,进而得出∠AMN+∠ANM=2(∠AA′M+∠A″)即可得出答案:
如图,作A关于BC和ED的对称点A′,A″,连接A′A″,交BC于M,交CD于N,

则A′A″即为△AMN的周长最小值。作DA延长线AH。
∵∠BAD=120°,∴∠HAA′=60°。
∴∠AA′M+∠A″=∠HAA′=60°。
∵∠MA′A=∠MAA′,∠NAD=∠A″,
且∠MA′A+∠MAA′=∠AMN,
∠NAD+∠A″=∠ANM,
∴∠AMN+∠ANM=∠MA′A+∠MAA′+∠NAD+∠A″=2(∠AA′M+∠A″)=2×60°=120°。
故选B。


科目:初中数学 来源: 题型:
【题目】乘法公式的探究及应用.
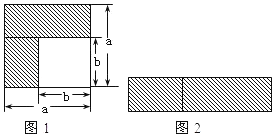
(1)如图1,可以求出阴影部分的面积是 (写成两数平方差的形式);
(2)如图2,若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是 ,长是 ,面积是 (写成多项式乘法的形式);
(3)比较图1、图2阴影部分的面积,可以得到公式 ;
(4)运用你所得到的公式,计算下列各题:
①10.2×9.8,②(2m+n﹣p)(2m﹣n+p).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,以B为圆心,BC长为半径画弧,分别交AC,AB于D,E,连接BD,DE,若∠A=30°,AB=AC,则∠BDE的度数为( ).

A.52.5°B.60°C.67.5°D.75°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一块长和宽分别为60厘米和40厘米的长方形铁皮,要在它的四角截去四个相等的小正方形,折成一个无盖的长方体水槽,使它的底面积为800平方厘米.求截去正方形的边长.

查看答案和解析>>
科目:初中数学 来源: 题型:
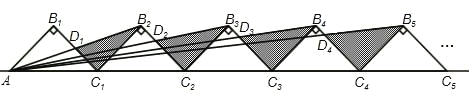
【题目】如图所示,n+1个直角边长为1的等腰直角三角形,斜边在同一直线上,设△B2D1C1的面积为S1,△B3D2C2的面积为S2,…,△Bn+1DnCn的面积为Sn,则S1= ,Sn= (用含n的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AM∥BN,∠A=60°,点P是射线AM上一动点(与点A不重合),BC,BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
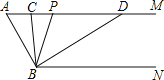
(1)求∠CBD的度数;
(2)当点P运动时,∠APB:∠ADB的比值是否随之变化?若不变,请求出这个比值;若变化,请找出变化规律;
(3)当点P运动到某处时,∠ACB=∠ABD,求此时∠ABC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
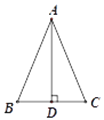
【题目】如图,AD是△ABC的边BC上的高,再添加下列条件中的某一个就能推出△ABC是等腰三角形.①BD=CD;②∠BAD=∠CAD;③AB+BD=AC+CD; ④AB-BD=AC-CD;⑤∠BAD=∠ACD.可以添加的条件序号正确答案是( )
A.①②B.①②③C.①②③④D.①②③④⑤.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将三角形纸片ABC沿AD折叠,使点C落在BD边上的点E处.若BC=8,BE=2.则AB2﹣AC2的值为( )
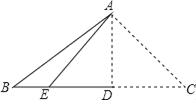
A. 4 B. 6 C. 10 D. 16
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com