
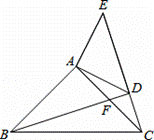
如图,已知:在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD.图中的CE、BD有怎样的大小和位置关系?试证明你的结论.
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案科目:初中数学 来源: 题型:
如图,正六边形ABCDEF的边长为2 ,延长BA,EF交于点O.以O为原点,以边AB所在的直线为x轴建立平面直角坐标系,
,延长BA,EF交于点O.以O为原点,以边AB所在的直线为x轴建立平面直角坐标系,
(1) OB=
(2) 直线AC与直线DB的交点坐标是(_____,_____).

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在△ABC中,AD是BC边上的中线,点E、F是AD的三等分点,若△ABC的面积为12cm2,则图中阴影部分的面积为( )
A.2cm2 B.4cm2 C.6cm2 D.8cm2
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
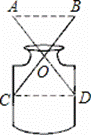
小红家有一个小口瓶(如图所示),她很想知道它的内径是多少?但是尺子不能伸在里边直接测,于是她想了想,唉!有办法了.她拿来了两根长度相同的细木条,并且把两根长木条的中点固定在一起,木条可以绕中点转动,这样只要量出AB的长,就可以知道玻璃瓶的内径是多少,你知道这是为什么吗?请说明理由.(木条的厚度不计)
查看答案和解析>>
科目:初中数学 来源: 题型:
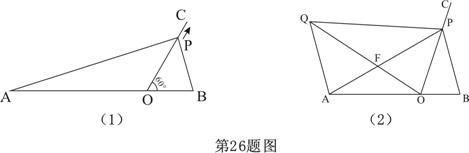
如图(1),线段AB与射线OC相交于点O,且∠BOC=60°,AO=3,OB=1,动点P以每秒1个单位长度的速度从点O出发,在射线OC做匀速运动,设运动时间为t秒.
(1)当t=3秒时,则OP= ,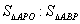 = ;
= ;
(2)当△OPB是直角三角形时,求t的值;
(3)如图(2),当AP=AB,过点A作AQ∥BP,并使得∠QOP=∠B,连接QP,QO、AP交于点F,试证明△APQ∽△BPO。
查看答案和解析>>
科目:初中数学 来源: 题型:
张师傅驾车运送货物到某地出售,汽车出发前油箱有油50升,行驶若干小时后,途中在加油站加油若干升,油箱中剩余油量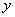 (升)与行驶时间
(升)与行驶时间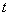 (小时)之间的关系如图所示。
(小时)之间的关系如图所示。
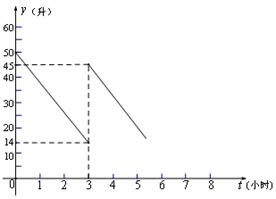
请根据图象回答下列问题:
(1)汽车行驶 小时后加油,
中途加油 升;
(2)已知加油前、后汽车都以70千米/小时匀速行驶,如果加油站距目的地210千米,要到达目的地,问油箱中的油是否够用?请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com