
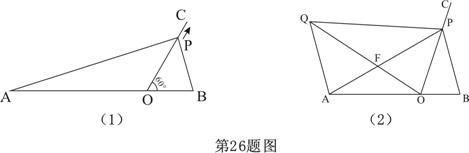
如图(1),线段AB与射线OC相交于点O,且∠BOC=60°,AO=3,OB=1,动点P以每秒1个单位长度的速度从点O出发,在射线OC做匀速运动,设运动时间为t秒.
(1)当t=3秒时,则OP= ,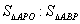 = ;
= ;
(2)当△OPB是直角三角形时,求t的值;
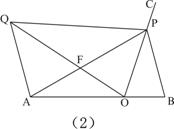
(3)如图(2),当AP=AB,过点A作AQ∥BP,并使得∠QOP=∠B,连接QP,QO、AP交于点F,试证明△APQ∽△BPO。
解:(1)OP=3,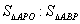 =3:4 4分
=3:4 4分
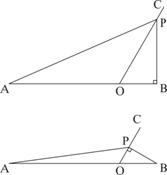 (2)①∵∠BOP=60°∴∠BOP不为直角; 5分
(2)①∵∠BOP=60°∴∠BOP不为直角; 5分
②当∠OBP=90°时,如图所示
∵∠BOP=60°∴∠OPB=30°
∴OP=2OB,
∴t=2s 7分
③当∠OPB=90°时,如图所示
∵∠BOP=60°∴∠OBP=30°
∴OB=2OP,
∴2t=1 ∴t=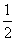 s 8分
s 8分
综上,当△OPB为直角三角形时,t=2s或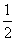 s 9分
s 9分
(3) ∵AQ∥BP,
∴ ∠QAP=∠APB
 ∵ AP=AB
∵ AP=AB
∴∠APB=∠B ∴ ∠QAP=∠B
又∵ ∠QOP=∠B
∴ ∠QAP=∠QOP
又∵∠QFA=∠PFO
∴ △QFA∽△PFO
∴ 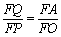 , 11分
, 11分
即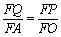 12分
12分
又∵ ∠PFQ=∠OFA,
∴ △PFQ∽△OFA 13分
∴ ∠QPA=∠QOA.
∵ ∠AOC=∠OPB+∠B=∠QOA+∠QOP,∠B=∠QOP,
∴∠QOA=∠OPB ∴∠OPB =∠QPA.
∴ △APQ∽△BPO.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
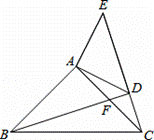
如图,已知:在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD.图中的CE、BD有怎样的大小和位置关系?试证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
对于同一平面内的三条直线a、b、c,给出5种论断:①a∥b;②b∥c;③a⊥b;④a∥c;⑤a⊥c,以其中两个为条件,一个为结论,组成一个你认为正确的命题
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知A,B两点在数轴上,点A表示的数为-10,OB=3OA,点M以每秒3个单位长度的速度从点A向右运动.点N以每秒2个单位长度的速度从点O向右运动(点M、点N同时出发)
(1)数轴上点B对应的数是______.
(2)经过几秒,点M、点N分别到原点O的距离相等?
(3)当点M运动到什么位置时,恰好使AM=2BN?(12分)
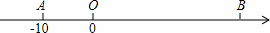
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com