练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】若方程x2+kx+9=0有两个相等的实数根，则k= ．

    【答案】±6
    【解析】解：∵方程x2+kx+9=0有两个相等的实数根， ∴△=0，即k2﹣419=0，解得k=±6．
    故答案为±6．
    根据根判别式△=b2﹣4ac的意义得到△=0，即k2﹣4×1×9=0，然后解方程即可．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】若⊙O1、⊙O2的半径分别为4和6，圆心距O1O2=8，则⊙O1与⊙O2的位置关系是（ ）
    A.内切
    B.相交
    C.外切
    D.外离

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如果∠A和∠B互为余角，∠A和∠C互为补角，∠B与∠C的和等于120°，那么这三个角分别是（ ）．
    A.50°，30°，130°;
    B.75°，15°，105°;
    C.60°，30°，120°;
    D.70°，20°，110°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某商品的进价为每件40元，当售价为每件60元时，每星期可卖出300件，现需降价处理，且经市场调查，每降价1元，每星期可多卖出20件，在确保盈利的前提下，解答下列问题：

    （1）若设每件降价x（x为整数）元，每星期售出商品的利润为y元，请写出x与y之间的函数关系式，并求出自变量x的取值范围；

    （2）请画出上述函数的大致图象.

    （3）当降价多少元时，每星期的利润最大？最大利润是多少？

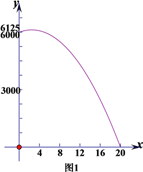
    小丽解答过程如下：

    解：（1）根据题意，可列出表达式：

    y=(60-x)(300+20x)-40(300+20x),

    即y=-20x2+100x+6000.

    ∵降价要确保盈利，∴40＜60-x60.解得0x＜20.

    （2）上述表达式的图象是抛物线的一部分，函数的大致图象如图1：

    （3）∵a=-20＜0，

    ∴当x==2.5时，y有最大值，y==6125.

    所以，当降价2.5元时，每星期的利润 最大，最大利润为6125.

    老师看了小丽的解题过程，说小马第（1）问的表达式是正确的，但自变量x的取值范围不准确.（2）（3）问的答案，也都存在问题.请你就老师说的问题，进行探究，写出你认为（1）（2）（3）中正确的答案，或说明错误原因.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知二次函数y=x2+bx-3的图象过点(1,0)．求该二次函数的解析式和顶点坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列抛物线中,过原点的抛物线是（ ）

    A.y 4x 2 1B.y 4x 2 1C.y 4(x 1) 2D.y 4x 2 x

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】对于二次函数y＝－x2＋2x，有下列四个结论：①它的对称轴是直线x＝1；②设y1＝－＋2x1，y2＝－＋2x2，则当x2＞x1时，有y2＞y1；③它的图象与x轴的两个交点是(0，0)和(2，0)；④当0＜x＜2时，y＞0.其中正确结论的个数为(　　)

    A. 1 B. 2 C. 3 D. 4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在同一平面内，∠A的两边分别与∠B的两边平行，且∠A比∠B的3倍少40°，则∠A =_______

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知等腰三角形的两边分别是4和9，则该等腰三角形的周长为_____．

    查看答案和解析>>

    同步练习册答案