
【题目】某中学九(1)班数学兴趣小组对本班同学一天饮用饮品的情况进行了调查,大致可分为四种:![]() :自带白开水;
:自带白开水;![]() :瓶装矿泉水;
:瓶装矿泉水;![]() :碳酸饮料;
:碳酸饮料;![]() :非碳酸饮料.根据统计结果绘制如下两个统计图,请根据统计图提供的信息,解答下列问题:
:非碳酸饮料.根据统计结果绘制如下两个统计图,请根据统计图提供的信息,解答下列问题:
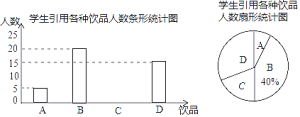
(1)请你补全条形统计图;
(2)为了养成良好的生活习惯,班主任决定在自带白开水的5名同学(男生2人,女生3人)中随机抽取2名同学担任生活监督员,请用列表法或树状图法求出恰好抽到一男一女的概率.
【答案】(1)补全条形统计图见解析;(2)![]() (恰好抽到一男一女)
(恰好抽到一男一女)![]() .
.
【解析】
(1)先根据B所占的百分比及相应的人数求出总人数,然后即可求出C类所对应的人数,即可补全条形统计图;
(2)用树状图或列表法找出所有的情况数,然后从中找出恰好抽到一男一女的情况数,利用所求情况数与总数之比求概率即可.
(1)![]() 抽查的总人数为:
抽查的总人数为:![]() (人),
(人),
![]() 类人数
类人数![]() (人),
(人),
补全条形统计图如下:
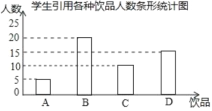
(2)列表得
女 | 女 | 女 | 男 | 男 | |
女 | --- | (女,女) | (女,女) | (男,女) | (男,女) |
女 | (女,女) | --- | (女,女) | (男,女) | (男,女) |
女 | (女,女) | (女,女) | --- | (男,女) | (男,女) |
男 | (女,男) | (女,男) | (女,男) | --- | (男,男) |
男 | (女,男) | (女,男) | (女,男) | (男,男) | --- |
或画树状图得:
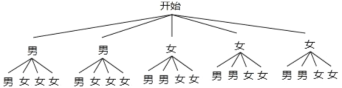
所有等可能的情况数有20种,其中一男一女的有12种,所以![]() (恰好抽到一男一女)
(恰好抽到一男一女)![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】小明在一次数学兴趣小组活动中,对一个数学问题作如下探究:
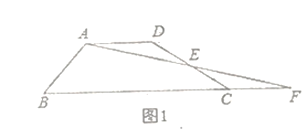
问题情境:(1)如图1,四边形![]() 中,
中,![]() ,点
,点![]() 为
为![]() 边的中点,连接
边的中点,连接![]() 并延长交
并延长交![]() 的延长线于点
的延长线于点![]() ,求证:
,求证:![]() ;(
;(![]() 表示面积)
表示面积)
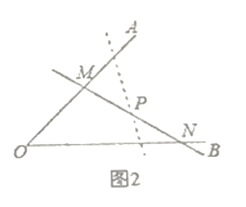
问题迁移:(2)如图2:在已知锐角![]() 内有一个定点
内有一个定点![]() .过点
.过点![]() 任意作一条直线
任意作一条直线![]() 分别交射线
分别交射线![]() 于点
于点![]() .小明将直线
.小明将直线![]() 绕着点
绕着点![]() 旋转的过程中发现,
旋转的过程中发现,![]() 的面积存在最小值,请问当直线
的面积存在最小值,请问当直线![]() 在什么位置时,
在什么位置时,![]() 的面积最小,并说明理由.
的面积最小,并说明理由.
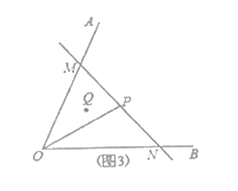
实际应用:(3)如图3,若在道路![]() 之间有一村庄
之间有一村庄![]() 发生疫情,防疫部门计划以公路
发生疫情,防疫部门计划以公路![]() 和经过防疫站
和经过防疫站![]() 的一条直线
的一条直线![]() 为隔离线,建立个面积最小的三角形隔离区
为隔离线,建立个面积最小的三角形隔离区![]() ,若测得
,若测得![]() 试求
试求![]() 的面积.(结果保留根号)(参考数据:
的面积.(结果保留根号)(参考数据:![]() )
)
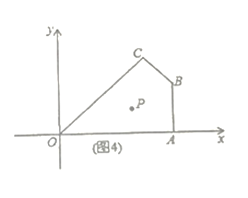
拓展延伸:(4)如图4,在平面直角坐标系中,![]() 为坐标原点,点
为坐标原点,点![]() 的坐标分别为
的坐标分别为![]() ,过点
,过点![]() 的直线
的直线![]() 与四边形
与四边形![]() 一组对边相交,将四边形
一组对边相交,将四边形![]() 分成两个四边形,求其中以点
分成两个四边形,求其中以点![]() 为顶点的四边形面积的最大值.
为顶点的四边形面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一副三角尺按如图①方式拼接:含30°角的三角尺的长直角边与含45°角的三角尺的斜边恰好重合(在Rt△ABC中,∠ACB=90°,∠BAC=30°;在Rt△ACD中,∠ADC=90°∠DAC=45°)已知AB=2![]() ,P是AC上的一个动点.
,P是AC上的一个动点.

(1)当PD=BC时,求∠PDA的度数;
(2)如图②,若E是CD的中点,求△DEP周长的最小值;
(3)如图③,当DP平分∠ADC时,在△ABC内存在一点Q,使得∠DQC=∠DPC,且CQ=![]() ,求PQ的长.
,求PQ的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
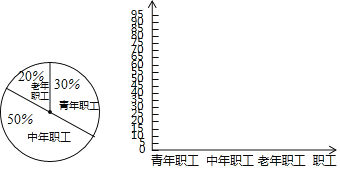
【题目】某单位有职工200人,其中青年职工(20﹣35岁),中年职工(35﹣50岁),老年职工(50岁及 以上)所占比例如扇形统计图所示.
为了解该单位职工的健康情况,小张、小王和小李各自对单位职工进行了抽样调查,将收集的数据进行了整理,绘制的统计表分别为表1、表2和表3.
表1:小张抽样调查单位3名职工的健康指数
年龄 | 26 | 42 | 57 |
健康指数 | 97 | 79 | 72 |
表2:小王抽样调查单位10名职工的健康指数
年龄 | 23 | 25 | 26 | 32 | 33 | 37 | 39 | 42 | 48 | 52 |
健康指数 | 93 | 89 | 90 | 83 | 79 | 75 | 80 | 69 | 68 | 60 |
表3:小李抽样调查单位10名职工的健康指数
年龄 | 22 | 29 | 31 | 36 | 39 | 40 | 43 | 46 | 51 | 55 |
健康指数 | 94 | 90 | 88 | 85 | 82 | 78 | 72 | 76 | 62 | 60 |
根据上述材料回答问题:
(1)小张、小王和小李三人中,谁的抽样调查的数据能够较好地反映出该单位职工健康情况,并简要说明其他两位同学抽样调查的不足之处.
(2)根据能够较好地反映出该单位职工健康情况表,绘制出青年职工、中年职工、老年职工健康指数的平均数的直方图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A、C分别在坐标轴上,点B的坐标为(4,2),直线![]() 交AB,BC分别于点M,N,反比例函数
交AB,BC分别于点M,N,反比例函数![]() 的图象经过点M,N.
的图象经过点M,N.

(1)求反比例函数的解析式;
(2)若点P在y轴上,且△OPM的面积与四边形BMON的面积相等,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为出行方便,近日来越来越多的重庆市民使用起了共享单车,图1为单车实物图,图2为单车示意图,AB与地面平行,点A、B、D共线,点D、F、G共线,坐垫C可沿射线BE方向调节.已知∠ABE=70°,∠EAB=45°,车轮半径为30cm,BE=40cm.小明体验后觉得当坐垫C离地面高度为0.9m时,骑着比较舒适,此时CE的长约为( )(结果精确到1cm,参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75,![]() ≈1.41)
≈1.41)
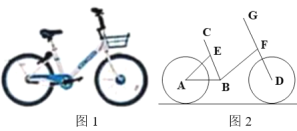
A.26cmB.24cmC.22cmD.20cm
查看答案和解析>>
科目:初中数学 来源: 题型:
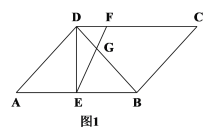
【题目】在平行四边形ABCD中,AD=BD,E为AB的中点,F为CD上一点,连接EF交BD于G.
(1)如图1,若DF=DG=2,AB=8,求EF的长;
(2)如图2,∠ADB=90°,点P为平行四边形ABCD外部一点,且AP=AD,连接BP、DP、EP,DP交EF于点Q,若BP⊥DP,EF⊥EP,求证:DQ=PQ.
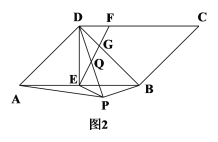
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB和抛物线的交点是A(0,-3),B(5,9),已知抛物线的顶点D的横坐标是2.

(1)求抛物线的解析式及顶点坐标;
(2)在![]() 轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
(3)在直线AB的下方抛物线上找一点P,连接PA,PB使得△PAB的面积最大,并求出这个最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为半圆O的直径,AC是⊙O的一条弦,D为![]() 的中点,作DE⊥AC于点E,交AB的延长线于点F,连结AD.
的中点,作DE⊥AC于点E,交AB的延长线于点F,连结AD.
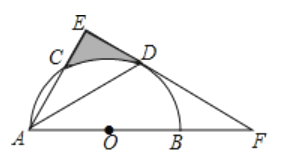
(1)求证:EF为半圆O的切线.
(2)若AO=BF=2,求阴影区域的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com