
【题目】在平面直角坐标系xOy中有不重合的两个点Q(x1,y1)与P(x2,y2),若Q、P为某个直角三角形的两个锐角顶点,且该直角三角形的直角边均与x轴或y轴平行(或重合),则我们将该直角三角形的两条直角边的边长之和称为点Q与点P之间的“直距”,记作DPQ,特别地,当PQ与某条坐标轴平行(或重合)时,线段PQ的长即为点Q与点P之间的“直距”,例如在图1中,点P(1,1),点Q(3,2),此时点Q与点P之间的“直距”DPQ=3.
(1)①已知O为坐标原点,点A(2,-1),B(-2,0),则DAO=________,DBO=________.
②点C在直线y=-x+3上,请你求出DCO的最小值.
(2)点E是以原点O为圆心,1为半径的圆上的一个动点,点F是直线y=2x+4上一动点,请你直接写出点E与点F之间“直距”DEF的最小值.
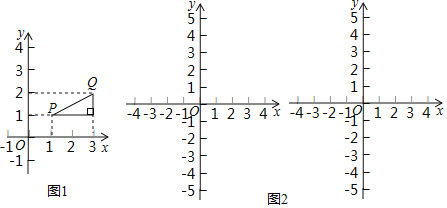
【答案】(1)①3,2;②最小值为3;(2)![]()
【解析】
(1)①根据点Q与点P之间的“直距”的定义计算即可;
②如图3中,由题意,当DCO为定值时,点C的轨迹是以点O为中心的正方形(如左边图),当DCO=3时,该正方形的一边与直线y=-x+3重合(如右边图),此时DCO定值最小,最小值为3;
(2)如图4中,平移直线y=2x+4,当平移后的直线与⊙O在左边相切时,设切点为E,作EF∥x轴交直线y=2x+4于F,此时DEF定值最小;
解:(1)①如图2中,
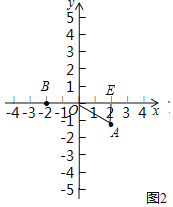
观察图象可知DAO=2+1=3,DBO=2,
故答案为3,2.
②如图3中,由题意,当DCO为定值时,点C的轨迹是以点O为中心的正方形(如左边图),
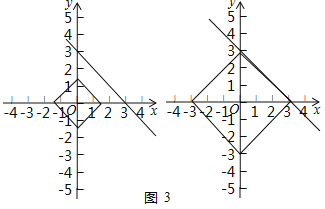
当DCO=3时,该正方形的一边与直线y=-x+3重合(如右边图),
此时DCO定值最小,最小值为3.
(2)如图4中,
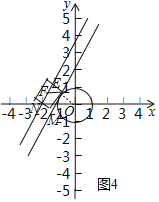
平移直线y=2x+4,当平移后的直线与⊙O在左边相切时,设切点为E,作EF∥x轴交直线y=2x+4于F,此时DEF定值最小,
因为直线y=2x+4与x轴交于N(-2,0),平移后的直线交x轴于M(![]() ,0),
,0),
∴ON=2,![]() ,
,
∴![]() .
.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
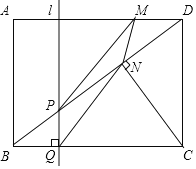
【题目】如图,在矩形ABCD中,CD=3cm,BC=4cm,连接BD,并过点C作CN⊥BD,垂足为N,直线l垂直BC,分别交BD、BC于点P、Q.直线l从AB出发,以每秒1cm的速度沿BC方向匀速运动到CD为止;点M沿线段DA以每秒1cm的速度由点D向点A匀速运动,到点A为止,直线1与点M同时出发,设运动时间为t秒(t>0).
(1)线段CN= ;
(2)连接PM和QN,当四边形MPQN为平行四边形时,求t的值;
(3)在整个运动过程中,当t为何值时△PMN的面积取得最大值,最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
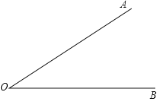
【题目】下面是小华设计的“作一个角等于已知角的2倍”的尺规作图过程.
已知:![]() .
.
求作:![]() ,使得
,使得![]() .
.
作法:如图,
①在射线![]() 上任取一点
上任取一点![]() ;
;
②作线段![]() 的垂直平分线,交
的垂直平分线,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ;
;
③连接![]() ;
;
所以![]() 即为所求作的角.
即为所求作的角.
根据小华设计的尺规作图过程,
(1)使用直尺和圆规补全图形(保留作图痕迹);
(2)完成下面的证明(说明:括号里填写推理的依据).
证明:∵![]() 是线段
是线段![]() 的垂直平分线,
的垂直平分线,
∴![]() ______(______)
______(______)
∴![]() .
.
∵![]() (______)
(______)
∴![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明为今年将要参加中考的好友小李制作了一个(如图)正方体礼品盒,六面上各有一字,连起来就是“预祝中考成功”,其中“预”的对面是“中”,“成”的对面是“功”,则它的平面展开图可能是( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
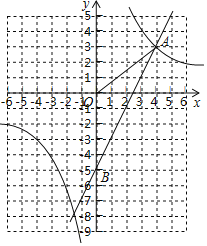
【题目】如图,一次函数y=kx+b的图象与反比例函数![]() 的图象交于点A(4,3),与y轴的负半轴交于点B,连接OA,且OA=OB.
的图象交于点A(4,3),与y轴的负半轴交于点B,连接OA,且OA=OB.
(1)求一次函数和反比例函数的表达式;
(2)过点P(k,0)作平行于y轴的直线,交一次函数y=2x+n于点M,交反比例函数![]() 的图象于点N,若NM=NP,求n的值.
的图象于点N,若NM=NP,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国为了实现到2020年达到全面小康社会的目标,近几年加大了扶贫工作的力度,合肥市某知名企业为了帮助某小型企业脱贫,投产一种书包,每个书包制造成本为18元,试销过程中发现,每月销售量y(万个)与销售单价x(元)之间的关系可以近似看作一次函数y=kx+b,据统计当售价定为30元/个时,每月销售40万个,当售价定为35元/个时,每月销售30万个.
(1)请求出k、b的值.
(2)写出每月的利润w(万元)与销售单价x(元)之间的函数解析式.
(3)该小型企业在经营中,每月销售单价始终保持在25≤x≤36元之间,求该小型企业每月获得利润w(万元)的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
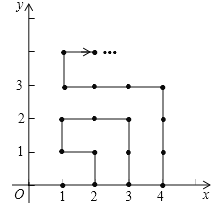
【题目】如图,在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(1,1),(1,2),(2,2)…根据这个规律,第2014个点的横坐标为_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某村在推进美丽乡村的活动中,决定建设幸福广场,计划铺设相同大小规格的红色和蓝色地砖.经过调查,获取信息如下:
购买数量低于5000块 | 购买数量不低于5000块 | |
红色地砖 | 原价销售 | 以八折销售 |
蓝色地砖 | 原价销售 | 以九折销售 |
如果购买红色地砖4000块,蓝色地砖6000块,需付款86000元;如果购买红色地砖10000块,蓝色地砖3500块,需付款99000元.则红色地砖与蓝色地砖的单价各为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与抛物线
与抛物线![]() 相交于A,B两点,且点A(1,-4)为抛物线的顶点,点B在x轴上。
相交于A,B两点,且点A(1,-4)为抛物线的顶点,点B在x轴上。

(1)求抛物线的解析式;
(2)在(1)中抛物线的第二象限图象上是否存在一点P,使△POB与△POC全等?若存在,求出点P的坐标;若不存在,请说明理由;
(3)若点Q是y轴上一点,且△ABQ为直角三角形,求点Q的坐标。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com