
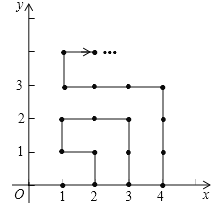
【题目】如图,在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(1,1),(1,2),(2,2)…根据这个规律,第2014个点的横坐标为_____________.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
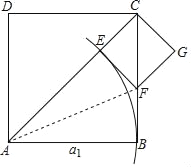
【题目】阅读下面材料:
已知:如图,在正方形ABCD中,边AB=a1.
按照以下操作步骤,可以从该正方形开始,构造一系列的正方形,它们之间的边满足一定的关系,并且一个比一个小.
操作步骤 | 作法 | 由操作步骤推断(仅选取部分结论) |
第一步 | 在第一个正方形ABCD的对角线AC上截取AE=a1,再作EF⊥AC于点E,EF与边BC交于点F,记CE=a2 | (i)△EAF≌△BAF(判定依据是①); (ii)△CEF是等腰直角三角形; (iii)用含a1的式子表示a2为②: |
第二步 | 以CE为边构造第二个正方形CEFG; | |
第三步 | 在第二个正方形的对角线CF上截取FH=a2,再作IH⊥CF于点H,IH与边CE交于点I,记CH=a3: | (iv)用只含a1的式子表示a3为③: |
第四步 | 以CH为边构造第三个正方形CHIJ | |
这个过程可以不断进行下去.若第n个正方形的边长为an,用只含a1的式子表示an为④ | ||
请解决以下问题:
(1)完成表格中的填空:
① ;② ;③ ;④ ;
(2)根据以上第三步、第四步的作法画出第三个正方形CHIJ(不要求尺规作图).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中有不重合的两个点Q(x1,y1)与P(x2,y2),若Q、P为某个直角三角形的两个锐角顶点,且该直角三角形的直角边均与x轴或y轴平行(或重合),则我们将该直角三角形的两条直角边的边长之和称为点Q与点P之间的“直距”,记作DPQ,特别地,当PQ与某条坐标轴平行(或重合)时,线段PQ的长即为点Q与点P之间的“直距”,例如在图1中,点P(1,1),点Q(3,2),此时点Q与点P之间的“直距”DPQ=3.
(1)①已知O为坐标原点,点A(2,-1),B(-2,0),则DAO=________,DBO=________.
②点C在直线y=-x+3上,请你求出DCO的最小值.
(2)点E是以原点O为圆心,1为半径的圆上的一个动点,点F是直线y=2x+4上一动点,请你直接写出点E与点F之间“直距”DEF的最小值.
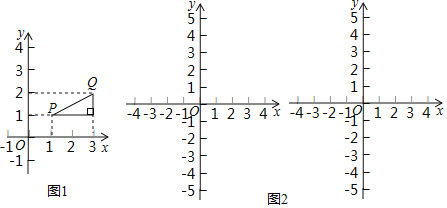
查看答案和解析>>
科目:初中数学 来源: 题型:
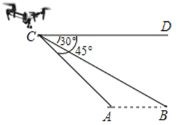
【题目】为开发大西北,某工程队承接高铁修筑任务,在山坡处需要修建隧道,为了测量隧道的长度,工程队用无人机在距地面高度为500米的C处测得山坡南北两端A、B的俯角分别为∠DCA=45°、∠DCB=30°(已知A、B、C三点在同一平面上),求隧道两端A、B的距离.(参考数据:![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径作圆O,分别交BC于点D,交CA的延长线于点E,过点D作DH⊥AC于点H,连接DE交线段OA于点F.
(1)求证:DH是圆O的切线;
(2)若A为EH的中点,求![]() 的值;
的值;
(3)若EA=EF=1,求圆O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=6,将△ABC绕点C按逆时针方向旋转得到△A'B'C',此时点A'恰好在AB边上,则点B'与点B之间的距离为( )
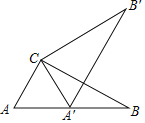
A. 12 B. 6 C. 6![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某中学学生课余生活情况,对喜爱看课外书、体育活动、看电视、社会实践四个方面的人数进行调查统计,现从该校随机抽取n名学生作为样本,采用问卷调查的方式收集数据![]() 参与问卷调查的每名学生只能选择其中一项
参与问卷调查的每名学生只能选择其中一项![]() ,并根据调查得到的数据绘制成了如图所示的两幅不完整的统计图,由图中提供的信息,解答下列问题:
,并根据调查得到的数据绘制成了如图所示的两幅不完整的统计图,由图中提供的信息,解答下列问题:
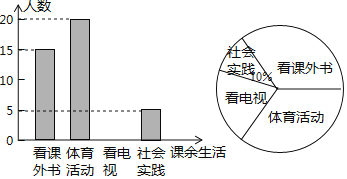
![]() 补全条形统计图;
补全条形统计图;
![]() 若该校共有学生2400名,试估计该校喜爱看电视的学生人数.
若该校共有学生2400名,试估计该校喜爱看电视的学生人数.
![]() 若调查到喜爱体育活动的4名学生中有3名男生和1名女生,现从这4名学生中任意抽取2名,求恰好抽到2名男生的概率.
若调查到喜爱体育活动的4名学生中有3名男生和1名女生,现从这4名学生中任意抽取2名,求恰好抽到2名男生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,点E是线段AC上一点,BE∥CD,∠BEC=∠BAD.
(1)如图1已知AB=AD;
①找出图中与∠DAC相等的角,并给出证明;
②求证:AE=CD;
(2)如图2,若BC∥ED,![]() ,∠BEC=45°,求tan∠ABE的值.
,∠BEC=45°,求tan∠ABE的值.
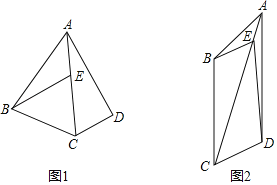
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com