
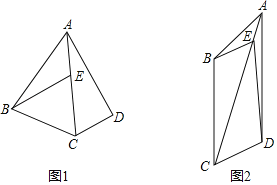
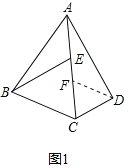
【题目】在四边形ABCD中,点E是线段AC上一点,BE∥CD,∠BEC=∠BAD.
(1)如图1已知AB=AD;
①找出图中与∠DAC相等的角,并给出证明;
②求证:AE=CD;
(2)如图2,若BC∥ED,![]() ,∠BEC=45°,求tan∠ABE的值.
,∠BEC=45°,求tan∠ABE的值.
【答案】(1)①∠ABE=∠CAD,理由详见解析;②详见解析;(2)![]() .
.
【解析】
(1)①证明△ABE≌△DAF,关键全等三角形的性质证明;
②根据全等三角形的性质证明结论;
(2)过点D作DG⊥CD交AC于点G,证明△ABE∽△DAG,得到![]() =
=![]() =
=![]() ,根据正切的定义计算,得到答案.
,根据正切的定义计算,得到答案.
解:(1)①∠ABE=∠CAD,
理由如下:以D为圆心,DC为半径画圆,交AC于F,连接DF,
则CD=DF,
∴∠DFC=∠DCF,
∵BE∥CD,
∴∠BEC=∠FCD,
∴∠BEC=∠DFC,
∴∠AEB=∠AFD,
∠BEC=∠BAE+∠ABE,∠BAD=∠BAE+∠DAF,∠BEC=∠BAD,
∴∠ABE=∠DAF,
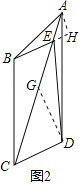
在△ABE和△DAF中,
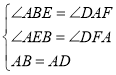 ,
,
∴△ABE≌△DAF(AAS),
∴∠ABE=∠CAD,
②∵△ABE≌△DAF,
∴AE=DF,
∵CD=DF,
∴AE=CD;
(3)过点D作DG⊥CD交AC于点G,
∵BE∥CD,
∴∠DCA=∠BEC=45°,
∴∠AEB=∠DGA=135°,DG=DC,
∵∠AEB=∠DGA,∠ABE=∠DAG,
∴△ABE∽△DAG,
∴![]() =
=![]() =
=![]() ,
,
∵BC∥DE,BE∥CD,
∴四边形BCDE为平行四边形,
∴BE=CD,
过点A作AH垂直于BE交BE的延长线于点H,
设AH=EH=m,
则AE=![]() m,DG=CD=BE=2
m,DG=CD=BE=2![]() m,
m,
∴BH=BE+EH=2![]() m+m,
m+m,
tan∠ABE=![]() =
=![]() =
=![]() .
.
故答案为:(1)①∠ABE=∠CAD,理由详见解析;②详见解析;(2)![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
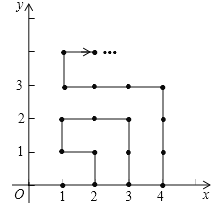
【题目】如图,在平面直角坐标系中,有若干个横坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(1,1),(1,2),(2,2)…根据这个规律,第2014个点的横坐标为_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠C=90°,AD⊥DB,点E为AB的中点,DE∥BC.
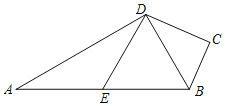
(1)求证:BD平分∠ABC;
(2)连接EC,若∠A=30°,DC=![]() ,求EC的长.
,求EC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与抛物线
与抛物线![]() 相交于A,B两点,且点A(1,-4)为抛物线的顶点,点B在x轴上。
相交于A,B两点,且点A(1,-4)为抛物线的顶点,点B在x轴上。

(1)求抛物线的解析式;
(2)在(1)中抛物线的第二象限图象上是否存在一点P,使△POB与△POC全等?若存在,求出点P的坐标;若不存在,请说明理由;
(3)若点Q是y轴上一点,且△ABQ为直角三角形,求点Q的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB<BC,点E为CD边的中点,连接AE并延长与BC的延长线交于点F,过点E作EM⊥AF交BC于点M,连接AM与BD交于点N,现有下列结论:①AM=MF;②ME2=MCAM;③![]() =(sin∠DAE)2;④点N是四边形ABME的外接圆的圆心,其中正确结论的序号是_____.
=(sin∠DAE)2;④点N是四边形ABME的外接圆的圆心,其中正确结论的序号是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
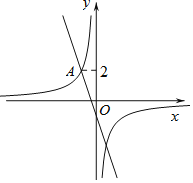
【题目】如图,在平面直角坐标系xOy中,直线![]() 与双曲线
与双曲线![]() 相交于点
相交于点![]() .
.
![]() 求双曲线
求双曲线![]() 的表达式;
的表达式;
![]() 过动点
过动点![]() 且垂直于x轴的直线与直线
且垂直于x轴的直线与直线![]() 及双曲线
及双曲线![]() 的交点分别为B和C,当点B位于点C下方时,求出n的取值范围.
的交点分别为B和C,当点B位于点C下方时,求出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在边长为5的正方形ABCD中,点E,F分别是BC,DC边上的两个动点(不与点B,C,D重合),且AE⊥EF.
(1)如图1,当BE=2时,求FC的长;
(2)延长EF交正方形ABCD外角平分线CP于点P.
①依题意将图2补全;
②小京通过观察、实验提出猜想:在点E运动的过程中,始终有AE=PE.小京把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的三种想法:
想法1:在AB上截取AG=EC,连接EG,要证AE=PE,需证△AGE≌△ECP.
想法2:作点A关于BC的对称点H,连接BH,CH,EH.要证AE=PE,需证△EHP为等腰三角形.
想法3:将线段BE绕点B顺时针旋转90°,得到线段BM,连接CM,EM,要证AE=PE,需证四边形MCPE为平行四边形.
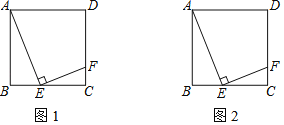
请你参考上面的想法,帮助小京证明AE=PE.(一种方法即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是矩形ABCD的边CD上一点,把△ADE沿AE对折,使点D恰好落在BC边上的F点处.已知折痕AE=10![]() ,且CE:CF=4:3,那么该矩形的周长为( )
,且CE:CF=4:3,那么该矩形的周长为( )
A.48B.64C.92D.96
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com