
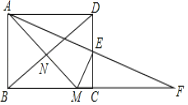
【题目】如图,在矩形ABCD中,AB<BC,点E为CD边的中点,连接AE并延长与BC的延长线交于点F,过点E作EM⊥AF交BC于点M,连接AM与BD交于点N,现有下列结论:①AM=MF;②ME2=MCAM;③![]() =(sin∠DAE)2;④点N是四边形ABME的外接圆的圆心,其中正确结论的序号是_____.
=(sin∠DAE)2;④点N是四边形ABME的外接圆的圆心,其中正确结论的序号是_____.

【答案】①②.
【解析】
①正确.利用全等三角形的性质证明AE=EF即可解决问题.
②正确.证明△MEC∽△MFE即可解决问题.
③错误.证明△ADE∽△ECM,可得![]() =(
=(![]() )2=(
)2=(![]() )2=(tan∠DAE)2.
)2=(tan∠DAE)2.
④错误.说明点N不是线段AM的中点,即可判断.
解:∵四边形ABC都是正方形,
∴AD∥BF,
∴∠DAE=∠F,
∵∠AED=∠FEC,DE=EC,
∴△ADE≌△FCE(AAS),
∴AE=EF,
∵ME⊥AF,
∴MA=NF,故①正确,
∵∠EMC=∠EMF,∠ECM=∠MEF,
∴△MEC∽△MFE,
∴ME:MF=MC:ME,
∴ME2=MCMF=MCAM,故②正确,
∵∠AEM=90°,∠ADE=∠ECM=90°,
∴∠AED+∠MEC=90°,∠MEC+∠EMC=90°,
∴∠AED=∠EMC,
∴△ADE∽△ECM,
∴![]() =(
=(![]() )2=(
)2=(![]() )2=(tan∠DAE)2,故③错误,
)2=(tan∠DAE)2,故③错误,
∵∠ABM=∠AEM=90°,
∴A,B,M,E四点共圆,
∴四边形的外接圆的圆心是线段AM的中点,显然点N不是AM的中点,故④错误.
故答案为①②.


科目:初中数学 来源: 题型:
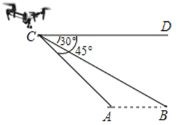
【题目】为开发大西北,某工程队承接高铁修筑任务,在山坡处需要修建隧道,为了测量隧道的长度,工程队用无人机在距地面高度为500米的C处测得山坡南北两端A、B的俯角分别为∠DCA=45°、∠DCB=30°(已知A、B、C三点在同一平面上),求隧道两端A、B的距离.(参考数据:![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据函数学习中积累的知识与经验,李老师要求学生探究函数y=![]() +1的图象.同学们通过列表、描点、画图象,发现它的图象特征,请你补充完整.
+1的图象.同学们通过列表、描点、画图象,发现它的图象特征,请你补充完整.
(1)函数y=![]() +1的图象可以由我们熟悉的函数 的图象向上平移 个单位得到;
+1的图象可以由我们熟悉的函数 的图象向上平移 个单位得到;
(2)函数y=![]() +1的图象与x轴、y轴交点的情况是: ;
+1的图象与x轴、y轴交点的情况是: ;
(3)请你构造一个函数,使其图象与x轴的交点为(2,0),且与y轴无交点,这个函数表达式可以是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
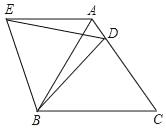
【题目】如图,在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60°,得到△BAE,连接ED,若BC=10,BD=9,则△ADE的周长为( )
A. 19B. 20C. 27D. 30
查看答案和解析>>
科目:初中数学 来源: 题型:
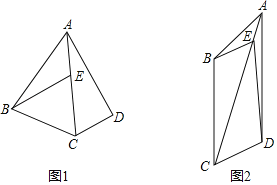
【题目】在四边形ABCD中,点E是线段AC上一点,BE∥CD,∠BEC=∠BAD.
(1)如图1已知AB=AD;
①找出图中与∠DAC相等的角,并给出证明;
②求证:AE=CD;
(2)如图2,若BC∥ED,![]() ,∠BEC=45°,求tan∠ABE的值.
,∠BEC=45°,求tan∠ABE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于任意三点A,B,C,给出如下定义:
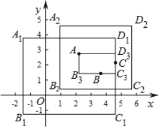
如果矩形的任何一条边均与某条坐标轴平行,且A,B,C三点都在矩形的内部或边界上,则称该矩形为点A,B,C的覆盖矩形.点A,B,C的所有覆盖矩形中,面积最小的矩形称为点A,B,C的最优覆盖矩形.例如,下图中的矩形A1B1C1D1,A2B2C2D2,AB3C3D3都是点A,B,C的覆盖矩形,其中矩形AB3C3D3是点A,B,C的最优覆盖矩形.
(1)已知A(﹣2,3),B(5,0),C(t,﹣2).
①当t=2时,点A,B,C的最优覆盖矩形的面积为 ;
②若点A,B,C的最优覆盖矩形的面积为40,求直线AC的表达式;
(2)已知点D(1,1).E(m,n)是函数y=![]() (x>0)的图象上一点,⊙P是点O,D,E的一个面积最小的最优覆盖矩形的外接圆,求出⊙P的半径r的取值范围.
(x>0)的图象上一点,⊙P是点O,D,E的一个面积最小的最优覆盖矩形的外接圆,求出⊙P的半径r的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】十八大报告首次提出建设生态文明,建设美丽中国.十九大报告再次明确,到2035年美丽中国目标基本实现.森林是人类生存发展的重要生态保障,提高森林的数量和质量对生态文明建设非常关键.截止到2013年,我国已经进行了八次森林资源清查,其中全国和北京的森林面积和森林覆盖率情况如下:
表1全国森林面积和森林覆盖率
清查次数 | 一 (1976年) | 二 (1981年) | 三 (1988年) | 四 (1993年) | 五 (1998年) | 六 (2003年) | 七 (2008年) | 八 (2013年) |
森林面积(万公顷) | 12200 | 1150 | 12500 | 13400 | 15894. 09 | 17490.92 | 19545.22 | 20768.73 |
森林覆盖率 | 12.7% | 12% | 12.98% | 13.92% | 16.55% | 18.21% | 20.36% | 21.63% |
表2北京森林面积和森林覆盖率
清查次数 | 一 (1976年) | 二 (1981年) | 三 (1988年) | 四 (1993年) | 五 (1998年) | 六 (2003年) | 七 (2008年) | 八 (2013年) |
森林面积(万公顷) | 33.74 | 37.88 | 52.05 | 58.81 | ||||
森林覆盖率 | 11.2% | 8.1% | 12.08% | 14.99% | 18.93% | 21.26% | 31.72% | 35.84% |
(以上数据来源于中国林业网)
请根据以上信息解答下列问题:
(1)从第 次清查开始,北京的森林覆盖率超过全国的森林覆盖率;
(2)补全以下北京森林覆盖率折线统计图,并在图中标明相应数据;

(3)第八次清查的全国森林面积20768.73(万公顷)记为a,全国森林覆盖率21.63%记为b,到2018年第九次森林资源清查时,如果全国森林覆盖率达到27.15%,那么全国森林面积可以达到 万公顷(用含a和b的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
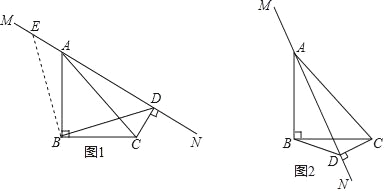
【题目】如图1,在Rt△ABC中,∠ABC=90°,BA=BC,直线MN是过点A的直线CD⊥MN于点D,连接BD.
(1)观察猜想张老师在课堂上提出问题:线段DC,AD,BD之间有什么数量关系.经过观察思考,小明出一种思路:如图1,过点B作BE⊥BD,交MN于点E,进而得出:DC+AD= BD.
(2)探究证明
将直线MN绕点A顺时针旋转到图2的位置写出此时线段DC,AD,BD之间的数量关系,并证明
(3)拓展延伸
在直线MN绕点A旋转的过程中,当△ABD面积取得最大值时,若CD长为1,请直接写BD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com