
【题目】十八大报告首次提出建设生态文明,建设美丽中国.十九大报告再次明确,到2035年美丽中国目标基本实现.森林是人类生存发展的重要生态保障,提高森林的数量和质量对生态文明建设非常关键.截止到2013年,我国已经进行了八次森林资源清查,其中全国和北京的森林面积和森林覆盖率情况如下:
表1全国森林面积和森林覆盖率
清查次数 | 一 (1976年) | 二 (1981年) | 三 (1988年) | 四 (1993年) | 五 (1998年) | 六 (2003年) | 七 (2008年) | 八 (2013年) |
森林面积(万公顷) | 12200 | 1150 | 12500 | 13400 | 15894. 09 | 17490.92 | 19545.22 | 20768.73 |
森林覆盖率 | 12.7% | 12% | 12.98% | 13.92% | 16.55% | 18.21% | 20.36% | 21.63% |
表2北京森林面积和森林覆盖率
清查次数 | 一 (1976年) | 二 (1981年) | 三 (1988年) | 四 (1993年) | 五 (1998年) | 六 (2003年) | 七 (2008年) | 八 (2013年) |
森林面积(万公顷) | 33.74 | 37.88 | 52.05 | 58.81 | ||||
森林覆盖率 | 11.2% | 8.1% | 12.08% | 14.99% | 18.93% | 21.26% | 31.72% | 35.84% |
(以上数据来源于中国林业网)
请根据以上信息解答下列问题:
(1)从第 次清查开始,北京的森林覆盖率超过全国的森林覆盖率;
(2)补全以下北京森林覆盖率折线统计图,并在图中标明相应数据;

(3)第八次清查的全国森林面积20768.73(万公顷)记为a,全国森林覆盖率21.63%记为b,到2018年第九次森林资源清查时,如果全国森林覆盖率达到27.15%,那么全国森林面积可以达到 万公顷(用含a和b的式子表示).
科目:初中数学 来源: 题型:
【题目】某数学社团成员想利用所学的知识测量某广告牌的宽度![]() 图中线段MN的长
图中线段MN的长![]() ,直线MN垂直于地面,垂足为点
,直线MN垂直于地面,垂足为点![]() 在地面A处测得点M的仰角为
在地面A处测得点M的仰角为![]() 、点N的仰角为
、点N的仰角为![]() ,在B处测得点M的仰角为
,在B处测得点M的仰角为![]() ,
,![]() 米,且A、B、P三点在一直线上
米,且A、B、P三点在一直线上![]() 请根据以上数据求广告牌的宽MN的长.
请根据以上数据求广告牌的宽MN的长.
![]() 参考数据:
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
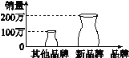
【题目】2018年某新品牌牛奶公司为了宣传其公司牛奶的销售量大,把该品牌牛奶的销售量与其他品牌牛奶的销售量对比绘制了如图K-28-3所示的广告,并形象地用牛奶瓶代替条形图,从销售量来看,新品牌牛奶的销售量是其他品牌牛奶的2倍.请分析这个图合理吗.
答:________,理由是______________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E、F分别在线BC、CD上运动,且满足∠EAF=45°,AE、AF分别与BD相交于点M、N.下列说法中:①BE+DF=EF;②点A到线段EF的距离一定等于正方形的边长;③若tan∠BAE=![]() ,则tan∠DAF=
,则tan∠DAF=![]() ;④若BE=2,DF=3,则S△AEF=18.其中结论正确的是__(将正确的序号写在横线上)
;④若BE=2,DF=3,则S△AEF=18.其中结论正确的是__(将正确的序号写在横线上)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场举办抽奖活动,规则如下:在不透明的袋子中有2个红球和2个黑球,这些球除颜色外都相同,顾客每次摸出一个球,若摸到红球,则获得1份奖品,若摸到黑球,则没有奖品。
(1)如果小芳只有一次摸球机会,那么小芳获得奖品的概率为 ;
(2)如果小芳有两次摸球机会(摸出后不放回),求小芳获得2份奖品的概率。(请用“画树状图”或“列表”等方法写出分析过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
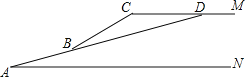
【题目】为提升城市品味、改善居民生活环境,我省某市拟对某条河沿线十余个地块进行片区改造,其中道路改造是难度较大的工程如图是某段河道坡路的横截面,从点A到点B,从点B到点C是两段不同坡度的坡路,CM是一段水平路段,CM与水平地面AN的距离为12米.已知山坡路AB的路面长10米,坡角BAN=15°,山坡路BC与水平面的夹角为30°,为了降低坡度,方便通行,决定降低坡路BC的坡度,得到新的山坡AD,降低后BD与CM相交于点D,点D,A,B在同一条直线上,即∠DAN=15°.为确定施工点D的位置,求整个山坡路AD的长和CD的长度(sin15°≈0.26,cos15°≈0.97,tan15°≈0.27,sin30°=0.50,cos30°≈0.87,tan30°≈0.58结果精确到0.1米)
查看答案和解析>>
科目:初中数学 来源: 题型:
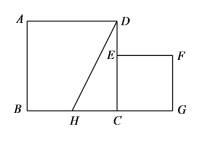
【题目】如图,已知正方形ABCD的边长为1,正方形CEFG的面积为![]() ,点E在CD边上,点G在BC的延长线上,设以线段AD和DE为邻边的矩形的面积为
,点E在CD边上,点G在BC的延长线上,设以线段AD和DE为邻边的矩形的面积为![]() ,且
,且![]() .
.
⑴求线段CE的长;
⑵若点H为BC边的中点,连结HD,求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com