
【题目】如图,正方形ABCD中,点E、F分别在线BC、CD上运动,且满足∠EAF=45°,AE、AF分别与BD相交于点M、N.下列说法中:①BE+DF=EF;②点A到线段EF的距离一定等于正方形的边长;③若tan∠BAE=![]() ,则tan∠DAF=
,则tan∠DAF=![]() ;④若BE=2,DF=3,则S△AEF=18.其中结论正确的是__(将正确的序号写在横线上)
;④若BE=2,DF=3,则S△AEF=18.其中结论正确的是__(将正确的序号写在横线上)

【答案】①②③.
【解析】
根据旋转的性质得到BH=DF,AH=AF,∠BAH=∠DAF,得到∠EAH=∠EAF=45°,根据全等三角形的性质得到EH=EF,∠AEB=∠AEF,于是得到BE+BH=BE+DF=EF,故①正确;过A作AG⊥EF于G,根据全等三角形的性质得到AB=AG,于是得到点A到线段EF的距离一定等于正方形的边长;故②正确;根据三角函数的定义设BE=m,AB=2m,求得CE=m,设DF=x,则CF=2m-x,EF=BE+DF=m+x,根据勾股定理得到x=![]() m,于是得到tan∠DAF=
m,于是得到tan∠DAF=![]() ;故正确;求得EF=BE+DF=5,设BC=CD=n,根据勾股定理即可得到结论.
;故正确;求得EF=BE+DF=5,设BC=CD=n,根据勾股定理即可得到结论.

解:如图,把△ADF绕点A顺时针旋转90°得到△ABH,
由旋转的性质得,BH=DF,AH=AF,∠BAH=∠DAF,
∵∠EAF=45°,
∴∠EAH=∠BAH+∠BAE=∠DAF+∠BAE=90°﹣∠EAF=45°,
∴∠EAH=∠EAF=45°,
在△AEF和△AEH中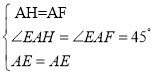 ,
,
∴△AEF≌△AEH(SAS),
∴EH=EF,
∴∠AEB=∠AEF,
∴BE+BH=BE+DF=EF,
故①正确;
过A作AG⊥EF于G,
∴∠AGE=∠ABE=90°,
在△ABE与△AGE中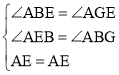 ,
,
∴△ABE≌△AGE(AAS),
∴AB=AG,
∴点A到线段EF的距离一定等于正方形的边长;故②正确;
∵tan∠BAE=![]() ,
,
∴设BE=m,AB=2m,
∴CE=m,
设DF=x,则CF=2m﹣x,EF=BE+DF=m+x,
∵CF2+CE2=EF2,
∴(2m﹣x)2+m2=(m+x)2,
∴x=![]() m,
m,
∴ ;故③正确;
;故③正确;
∵BE=2,DF=3,
∴EF=BE+DF=5,
设BC=CD=n,
∴CE=n﹣2,CF=n﹣3,
∴EF2=CE2+CF2,
∴25=(n﹣2)2+(n﹣3)2,
∴n=6(负值舍去),
∴AG=6,
∴![]() .故④错误,
.故④错误,
故答案为:①②③.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
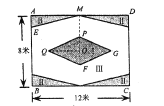
【题目】如图,某校准备给长12米,宽8米的矩形![]() 室内场地进行地面装饰,现将其划分为区域Ⅰ(菱形
室内场地进行地面装饰,现将其划分为区域Ⅰ(菱形![]() ),区域Ⅱ(4个全等的直角三角形),剩余空白部分记为区域Ⅲ;点
),区域Ⅱ(4个全等的直角三角形),剩余空白部分记为区域Ⅲ;点![]() 为矩形和菱形的对称中心,
为矩形和菱形的对称中心,![]() ,
,![]() ,
,![]() ,为了美观,要求区域Ⅱ的面积不超过矩形
,为了美观,要求区域Ⅱ的面积不超过矩形![]() 面积的
面积的![]() ,若设
,若设![]() 米.
米.
甲 | 乙 | 丙 | |
单价(元/米2) |
|
|
|
(1)当![]() 时,求区域Ⅱ的面积.
时,求区域Ⅱ的面积.
(2)计划在区域Ⅰ,Ⅱ分别铺设甲,乙两款不同的深色瓷砖,区域Ⅲ铺设丙款白色瓷砖,
①在相同光照条件下,当场地内白色区域的面积越大,室内光线亮度越好.当![]() 为多少时,室内光线亮度最好,并求此时白色区域的面积.
为多少时,室内光线亮度最好,并求此时白色区域的面积.
②三种瓷砖的单价列表如下,![]() 均为正整数,若当
均为正整数,若当![]() 米时,购买三款瓷砖的总费用最少,且最少费用为7200元,此时
米时,购买三款瓷砖的总费用最少,且最少费用为7200元,此时![]() __________,
__________,
查看答案和解析>>
科目:初中数学 来源: 题型:
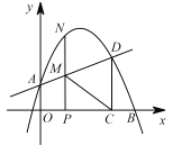
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+1交y轴于点A,交x轴正半轴于点B(4,0) ,与过A点的直线相交于另一点D(3,![]() ) ,过点D作DC⊥x轴,垂足为C.
) ,过点D作DC⊥x轴,垂足为C.
(1)求抛物线的表达式;
(2)点P在线段OC上(不与点O,C重合),过P作PN⊥x轴,交直线AD于M,交抛物线于点N,连接CM,求△PCM 面积的最大值;
(3)若P 是x 轴正半轴上的一动点,设OP 的长为t.是否存在t,使以点M,C,D,N 为顶点的四边形是平行四边形?若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的对角线交于O点,DE∥AC,CE∥BD,
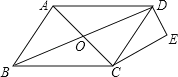
(1)求证:四边形OCED是矩形;
(2)若AD=5,BD=8,计算sin∠DCE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解决问题:
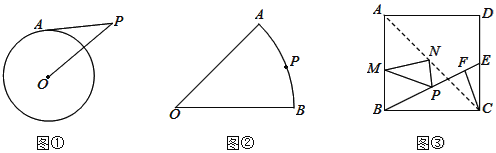
![]() 如图
如图![]() ,半径为4的
,半径为4的![]() 外有一点P,且
外有一点P,且![]() ,点A在
,点A在![]() 上,则PA的最大值和最小值分别是______和______.
上,则PA的最大值和最小值分别是______和______.
![]() 如图
如图![]() ,扇形AOB的半径为4,
,扇形AOB的半径为4,![]() ,P为弧AB上一点,分别在OA边找点E,在OB边上找一点F,使得
,P为弧AB上一点,分别在OA边找点E,在OB边上找一点F,使得![]() 周长的最小,请在图
周长的最小,请在图![]() 中确定点E、F的位置并直接写出
中确定点E、F的位置并直接写出![]() 周长的最小值;
周长的最小值;
拓展应用
![]() 如图
如图![]() ,正方形ABCD的边长为
,正方形ABCD的边长为![]() ;E是CD上一点
;E是CD上一点![]() 不与D、C重合
不与D、C重合![]() ,
,![]() 于F,P在BE上,且
于F,P在BE上,且![]() ,M、N分别是AB、AC上动点,求
,M、N分别是AB、AC上动点,求![]() 周长的最小值.
周长的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,点O在对角线BD上,以OD为半径的⊙O与AD、BD分别交于点E、F,且∠ABE=∠DBC.
![]()

(1)求证:BE与⊙O相切;
(2)若![]() ,CD=2,求⊙O的半径.
,CD=2,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】十八大报告首次提出建设生态文明,建设美丽中国.十九大报告再次明确,到2035年美丽中国目标基本实现.森林是人类生存发展的重要生态保障,提高森林的数量和质量对生态文明建设非常关键.截止到2013年,我国已经进行了八次森林资源清查,其中全国和北京的森林面积和森林覆盖率情况如下:
表1全国森林面积和森林覆盖率
清查次数 | 一 (1976年) | 二 (1981年) | 三 (1988年) | 四 (1993年) | 五 (1998年) | 六 (2003年) | 七 (2008年) | 八 (2013年) |
森林面积(万公顷) | 12200 | 1150 | 12500 | 13400 | 15894. 09 | 17490.92 | 19545.22 | 20768.73 |
森林覆盖率 | 12.7% | 12% | 12.98% | 13.92% | 16.55% | 18.21% | 20.36% | 21.63% |
表2北京森林面积和森林覆盖率
清查次数 | 一 (1976年) | 二 (1981年) | 三 (1988年) | 四 (1993年) | 五 (1998年) | 六 (2003年) | 七 (2008年) | 八 (2013年) |
森林面积(万公顷) | 33.74 | 37.88 | 52.05 | 58.81 | ||||
森林覆盖率 | 11.2% | 8.1% | 12.08% | 14.99% | 18.93% | 21.26% | 31.72% | 35.84% |
(以上数据来源于中国林业网)
请根据以上信息解答下列问题:
(1)从第 次清查开始,北京的森林覆盖率超过全国的森林覆盖率;
(2)补全以下北京森林覆盖率折线统计图,并在图中标明相应数据;

(3)第八次清查的全国森林面积20768.73(万公顷)记为a,全国森林覆盖率21.63%记为b,到2018年第九次森林资源清查时,如果全国森林覆盖率达到27.15%,那么全国森林面积可以达到 万公顷(用含a和b的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】□ABCD中,E、F是对角线BD上不同的两点,下列条件中,不能得出四边形AECF一定为平行四边形的是( )
A. BE=DF B. AE=CF C. AF//CE D. ∠BAE=∠DCF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某品牌自行车的最新车型实物图和简化图,它在轻量化设计、刹车、车篮和座位上都做了升级.A为后胎中心,经测量车轮半径AD为30cm,中轴轴心C到地面的距离CF为30cm,座位高度最低刻度为155cm,此时车架中立管BC长为54cm,且∠BCA=71°.(参考数据:sin71°≈0.95,cos71°≈0.33,tan71°≈2.88)
(1)求车座B到地面的高度(结果精确到1cm);
(2)根据经验,当车座B'到地面的距离B'E'为90cm时,身高175cm的人骑车比较舒适,此时车架中立管BC拉长的长度BB'应是多少?(结果精确到1cm)
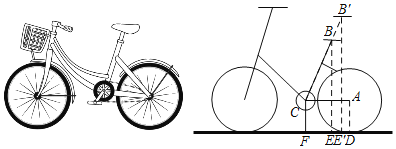
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com