
【题目】如图是某品牌自行车的最新车型实物图和简化图,它在轻量化设计、刹车、车篮和座位上都做了升级.A为后胎中心,经测量车轮半径AD为30cm,中轴轴心C到地面的距离CF为30cm,座位高度最低刻度为155cm,此时车架中立管BC长为54cm,且∠BCA=71°.(参考数据:sin71°≈0.95,cos71°≈0.33,tan71°≈2.88)
(1)求车座B到地面的高度(结果精确到1cm);
(2)根据经验,当车座B'到地面的距离B'E'为90cm时,身高175cm的人骑车比较舒适,此时车架中立管BC拉长的长度BB'应是多少?(结果精确到1cm)
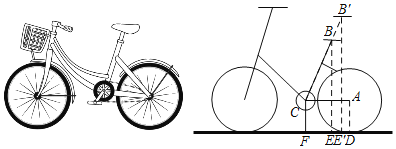
【答案】(1)车座B到地面的高度是81cm;(2)车架中立管BC拉长的长度BB'应是6cm.
【解析】
(1)根据上题证得的结论分别求得BH的长,利用正弦函数的定义即可得到结论;
(2)设B'E'与AC交于点H',则有B'H'∥BH,得到△B'H'C∽△BHC,利用相似三角形的性质求得BB'的长即可.
(1)设AC于BE交于H,
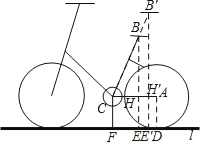
∵AD⊥l,CF⊥l,HE⊥l,
∴AD∥CF∥HE,
∵AD=30cm,CF=30cm,
∴AD=CF,
∴四边形ADFC是平行四边形,
∵∠ADF=90°,
∴四边形ADFC是矩形,
∴HE=AD=30cm,
∵BC长为54cm,且∠BCA=71°,
∴BH=BCsin71°=51.3cm,
∴BE=BH+EH=BH+AD=51.3+30≈81cm;
答:车座B到地面的高度是81cm;
(2)如图所示,B'E'=96.8cm,设B'E'与AC交于点H',则有B'H'∥BH,
∴△B'H'C∽△BHC,得![]() .
.
即![]() ,
,
∴B'C=cm.
故BB'=B'C﹣BC=60﹣54=6(cm).
∴车架中立管BC拉长的长度BB'应是6cm.


 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E、F分别在线BC、CD上运动,且满足∠EAF=45°,AE、AF分别与BD相交于点M、N.下列说法中:①BE+DF=EF;②点A到线段EF的距离一定等于正方形的边长;③若tan∠BAE=![]() ,则tan∠DAF=
,则tan∠DAF=![]() ;④若BE=2,DF=3,则S△AEF=18.其中结论正确的是__(将正确的序号写在横线上)
;④若BE=2,DF=3,则S△AEF=18.其中结论正确的是__(将正确的序号写在横线上)

查看答案和解析>>
科目:初中数学 来源: 题型:
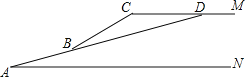
【题目】为提升城市品味、改善居民生活环境,我省某市拟对某条河沿线十余个地块进行片区改造,其中道路改造是难度较大的工程如图是某段河道坡路的横截面,从点A到点B,从点B到点C是两段不同坡度的坡路,CM是一段水平路段,CM与水平地面AN的距离为12米.已知山坡路AB的路面长10米,坡角BAN=15°,山坡路BC与水平面的夹角为30°,为了降低坡度,方便通行,决定降低坡路BC的坡度,得到新的山坡AD,降低后BD与CM相交于点D,点D,A,B在同一条直线上,即∠DAN=15°.为确定施工点D的位置,求整个山坡路AD的长和CD的长度(sin15°≈0.26,cos15°≈0.97,tan15°≈0.27,sin30°=0.50,cos30°≈0.87,tan30°≈0.58结果精确到0.1米)
查看答案和解析>>
科目:初中数学 来源: 题型:
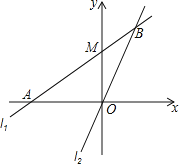
【题目】如图,在平面直角坐标系xOy中,过点A(﹣6,0)的直线l1与直线l2:y=2x相交于点B(m,6)
(1)求直线l1的表达式
(2)直线l1与y轴交于点M,求△BOM的面积;
(3)过动点P(m,0)且垂于x轴的直线与l1,l2的交点分别为C,D,当点C位于点D下方时,写出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在宣传“民族团结”活动中,采用四种宣传形式:A.器乐,B.舞蹈,C.朗诵,D.唱歌.每名学生从中选择并且只能选择一种最喜欢的,学校就宣传形式对学生进行了抽样调查,并将调查结果绘制了如下两幅不完整的统计图.

请结合图中所给信息,解答下列问题:
(1)本次调查的学生共有_____人;
(2)补全条形统计图;
(3)该校共有1200名学生,请估计选择“唱歌”的学生有多少人?
(4)七年一班在最喜欢“器乐”的学生中,有甲、乙、丙、丁四位同学表现优秀,现从这四位同学中随机选出两名同学参加学校的器乐队,请用列表或画树状图法求被选取的两人恰好是甲和乙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学社团成员想利用所学的知识测量某广告牌的宽度![]() 图中线段MN的长
图中线段MN的长![]() ,直线MN垂直于地面,垂足为点
,直线MN垂直于地面,垂足为点![]() 在地面A处测得点M的仰角为
在地面A处测得点M的仰角为![]() 、点N的仰角为
、点N的仰角为![]() ,在B处测得点M的仰角为
,在B处测得点M的仰角为![]() ,
,![]() 米,且A、B、P三点在一直线上
米,且A、B、P三点在一直线上![]() 请根据以上数据求广告牌的宽MN的长.
请根据以上数据求广告牌的宽MN的长.
![]() 参考数据:
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
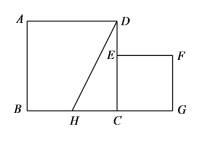
【题目】如图,已知正方形ABCD的边长为1,正方形CEFG的面积为![]() ,点E在CD边上,点G在BC的延长线上,设以线段AD和DE为邻边的矩形的面积为
,点E在CD边上,点G在BC的延长线上,设以线段AD和DE为邻边的矩形的面积为![]() ,且
,且![]() .
.
⑴求线段CE的长;
⑵若点H为BC边的中点,连结HD,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张老师计划到超市购买甲种文具100个,他到超市后发现还有乙种文具可供选择,如果调整文具的购买品种,每减少购买1个甲种文具,需增加购买2个乙种文具.设购买x个甲种文具时,需购买y个乙种文具.
(1)①当减少购买1个甲种文具时,x=______,y=________;
②求y与x之间的函数表达式.
(2)已知甲种文具每个5元,乙种文具每个3元,张老师购买这两种文具共用去540元,甲、乙两种文具各购买了多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
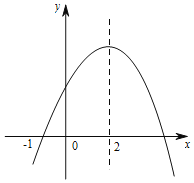
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(-1,0),对称轴为直线x=2,下列结论:(1)2a+b=0;(2)9a+c>3b;(3)5a+7b+2c>0;(4)若点A(-3,y1)、点B(![]() ,y2)、点C(
,y2)、点C(![]() ,y3)在该函数图象上,则y1<y2<y3;(5)若方程a(x+1)(x-5)=c的两根为x1和x2,且x1<x2,则x1<-1<5<x2,其中正确的结论有( )
,y3)在该函数图象上,则y1<y2<y3;(5)若方程a(x+1)(x-5)=c的两根为x1和x2,且x1<x2,则x1<-1<5<x2,其中正确的结论有( )
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com