
【题目】为提升城市品味、改善居民生活环境,我省某市拟对某条河沿线十余个地块进行片区改造,其中道路改造是难度较大的工程如图是某段河道坡路的横截面,从点A到点B,从点B到点C是两段不同坡度的坡路,CM是一段水平路段,CM与水平地面AN的距离为12米.已知山坡路AB的路面长10米,坡角BAN=15°,山坡路BC与水平面的夹角为30°,为了降低坡度,方便通行,决定降低坡路BC的坡度,得到新的山坡AD,降低后BD与CM相交于点D,点D,A,B在同一条直线上,即∠DAN=15°.为确定施工点D的位置,求整个山坡路AD的长和CD的长度(sin15°≈0.26,cos15°≈0.97,tan15°≈0.27,sin30°=0.50,cos30°≈0.87,tan30°≈0.58结果精确到0.1米)
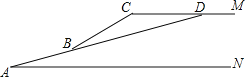
【答案】修整后山坡路AD的长约为46.2米,CD的长约为18.8米.
【解析】
过B作BE⊥AN于E,过D作DF⊥AN于F,过C作CG⊥AN于G,过B作BH⊥CG于H,根据矩形的性质得到BE=GH,EG=BH,CD=GF,CG=DF,求得CH=DF-GH,解直角三角形即可得到结论.
过B作BE⊥AN于E,过D作DF⊥AN于F,过C作CG⊥AN于G,过B作BH⊥CG于H,
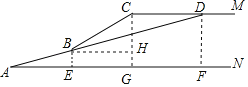
则四边形CGFD和四边形BEGH是矩形,
∴BE=GH,EG=BH,CD=GF,CG=DF,
∴CH=DF﹣GH,
由题意得,DF=12,AB=10,
在Rt△ABE中,BE=ABsin15°=10×0.26=2.6,
在Rt△ADF中,DF=ABsin15°,AD=12÷0.26=46.2,
∴CH=DF﹣BE=9.4,
在Rt△CBH中,CH=BCsin30°,BC=CH÷0.5=18.8,
∵CD∥AN,
∴∠CDB=∠BAN=15°,
∵∠CBH=30°,
∴∠DBC=15°,
∴∠CDB=∠CBD,
∴CD=CB=18.8(米),
答:修整后山坡路AD的长约为46.2米,CD的长约为18.8米.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+1交y轴于点A,交x轴正半轴于点B(4,0) ,与过A点的直线相交于另一点D(3,![]() ) ,过点D作DC⊥x轴,垂足为C.
) ,过点D作DC⊥x轴,垂足为C.
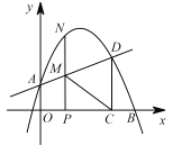
(1)求抛物线的表达式;
(2)点P在线段OC上(不与点O,C重合),过P作PN⊥x轴,交直线AD于M,交抛物线于点N,连接CM,求△PCM 面积的最大值;
(3)若P 是x 轴正半轴上的一动点,设OP 的长为t.是否存在t,使以点M,C,D,N 为顶点的四边形是平行四边形?若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】十八大报告首次提出建设生态文明,建设美丽中国.十九大报告再次明确,到2035年美丽中国目标基本实现.森林是人类生存发展的重要生态保障,提高森林的数量和质量对生态文明建设非常关键.截止到2013年,我国已经进行了八次森林资源清查,其中全国和北京的森林面积和森林覆盖率情况如下:
表1全国森林面积和森林覆盖率
清查次数 | 一 (1976年) | 二 (1981年) | 三 (1988年) | 四 (1993年) | 五 (1998年) | 六 (2003年) | 七 (2008年) | 八 (2013年) |
森林面积(万公顷) | 12200 | 1150 | 12500 | 13400 | 15894. 09 | 17490.92 | 19545.22 | 20768.73 |
森林覆盖率 | 12.7% | 12% | 12.98% | 13.92% | 16.55% | 18.21% | 20.36% | 21.63% |
表2北京森林面积和森林覆盖率
清查次数 | 一 (1976年) | 二 (1981年) | 三 (1988年) | 四 (1993年) | 五 (1998年) | 六 (2003年) | 七 (2008年) | 八 (2013年) |
森林面积(万公顷) | 33.74 | 37.88 | 52.05 | 58.81 | ||||
森林覆盖率 | 11.2% | 8.1% | 12.08% | 14.99% | 18.93% | 21.26% | 31.72% | 35.84% |
(以上数据来源于中国林业网)
请根据以上信息解答下列问题:
(1)从第 次清查开始,北京的森林覆盖率超过全国的森林覆盖率;
(2)补全以下北京森林覆盖率折线统计图,并在图中标明相应数据;

(3)第八次清查的全国森林面积20768.73(万公顷)记为a,全国森林覆盖率21.63%记为b,到2018年第九次森林资源清查时,如果全国森林覆盖率达到27.15%,那么全国森林面积可以达到 万公顷(用含a和b的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】□ABCD中,E、F是对角线BD上不同的两点,下列条件中,不能得出四边形AECF一定为平行四边形的是( )
A. BE=DF B. AE=CF C. AF//CE D. ∠BAE=∠DCF
查看答案和解析>>
科目:初中数学 来源: 题型:
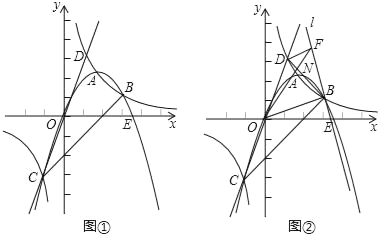
【题目】如图①,双曲线y=![]() (k≠0)和抛物线y=ax2+bx(a≠0)交于A、B、C三点,其中B(3,1),C(﹣1,﹣3),直线CO交双曲线于另一点D,抛物线与x轴交于另一点E.
(k≠0)和抛物线y=ax2+bx(a≠0)交于A、B、C三点,其中B(3,1),C(﹣1,﹣3),直线CO交双曲线于另一点D,抛物线与x轴交于另一点E.
(1)求双曲线和抛物线的解析式;
(2)抛物线在第一象限部分是否存在点P,使得∠POE+∠BCD=90°?若存在,请求出满足条件的点P的坐标;若不存在,请说明理由;
(3)如图②,过B作直线l⊥OB,过点D作DF⊥l于点F,BD与OF交于点N,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应市政府“绿色出行”的号召,小张上班由自驾车改为骑公共自行车.已知小张家距上班地点10千米.他用骑公共自行车的方式平均每小时行驶的路程比他用自驾车的方式平均每小时行驶的路程少45千米,他从家出发到上班地点,骑公共自行车方式所用的时间是自驾车方式所用的时间的4倍.设小张用骑公共自行车方式上班平均每小时行驶x千米,根据题意,可列方程为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=5cm,BD=8cm,动点P从点B开始沿BC边匀速运动,动点Q从点D开始沿对角线DB匀速运动,它们的运动速度均为1cm/s,过点Q作QE⊥CD,与CD交于点E,连接PQ,点P和点Q同时出发,设运动时间为t(s),0<t≤5.
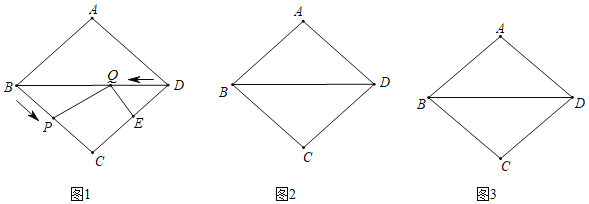
(1)当PQ∥CD时,求t的值;
(2)设四边形PQEC的面积为S(cm2),求S与t之间的函数关系式;
(3)当P,Q两点运动到使∠PQE=60°时,求四边形PQEC的面积;
(4)是否存在某一时刻t,使PQ+QE的值最小?若存在,请求t的值,并求出此时PQ+QE的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某品牌自行车的最新车型实物图和简化图,它在轻量化设计、刹车、车篮和座位上都做了升级.A为后胎中心,经测量车轮半径AD为30cm,中轴轴心C到地面的距离CF为30cm,座位高度最低刻度为155cm,此时车架中立管BC长为54cm,且∠BCA=71°.(参考数据:sin71°≈0.95,cos71°≈0.33,tan71°≈2.88)
(1)求车座B到地面的高度(结果精确到1cm);
(2)根据经验,当车座B'到地面的距离B'E'为90cm时,身高175cm的人骑车比较舒适,此时车架中立管BC拉长的长度BB'应是多少?(结果精确到1cm)
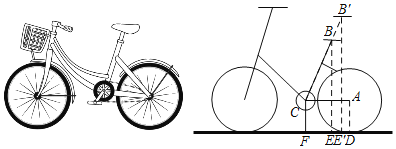
查看答案和解析>>
科目:初中数学 来源: 题型:
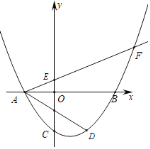
【题目】如图,在平面直角坐标系xOy中,已知抛物线![]() 与x轴交于点A、
与x轴交于点A、![]() 在B左侧
在B左侧![]() ,与y轴交于点C,经过点A的射线AF与y轴正半轴相交于点E,与抛物线的另一个交点为F,
,与y轴交于点C,经过点A的射线AF与y轴正半轴相交于点E,与抛物线的另一个交点为F,![]() ,点D是点C关于抛物线对称轴的对称点,点P是y轴上一点,且
,点D是点C关于抛物线对称轴的对称点,点P是y轴上一点,且![]() ,则点P的坐标是______.
,则点P的坐标是______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com