
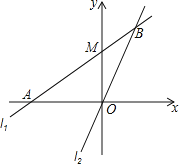
【题目】如图,在平面直角坐标系xOy中,过点A(﹣6,0)的直线l1与直线l2:y=2x相交于点B(m,6)
(1)求直线l1的表达式
(2)直线l1与y轴交于点M,求△BOM的面积;
(3)过动点P(m,0)且垂于x轴的直线与l1,l2的交点分别为C,D,当点C位于点D下方时,写出n的取值范围.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的对角线交于O点,DE∥AC,CE∥BD,
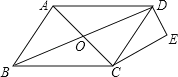
(1)求证:四边形OCED是矩形;
(2)若AD=5,BD=8,计算sin∠DCE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】□ABCD中,E、F是对角线BD上不同的两点,下列条件中,不能得出四边形AECF一定为平行四边形的是( )
A. BE=DF B. AE=CF C. AF//CE D. ∠BAE=∠DCF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应市政府“绿色出行”的号召,小张上班由自驾车改为骑公共自行车.已知小张家距上班地点10千米.他用骑公共自行车的方式平均每小时行驶的路程比他用自驾车的方式平均每小时行驶的路程少45千米,他从家出发到上班地点,骑公共自行车方式所用的时间是自驾车方式所用的时间的4倍.设小张用骑公共自行车方式上班平均每小时行驶x千米,根据题意,可列方程为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=5cm,BD=8cm,动点P从点B开始沿BC边匀速运动,动点Q从点D开始沿对角线DB匀速运动,它们的运动速度均为1cm/s,过点Q作QE⊥CD,与CD交于点E,连接PQ,点P和点Q同时出发,设运动时间为t(s),0<t≤5.
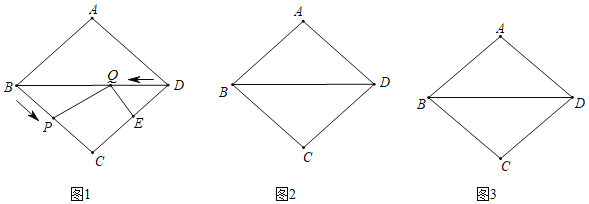
(1)当PQ∥CD时,求t的值;
(2)设四边形PQEC的面积为S(cm2),求S与t之间的函数关系式;
(3)当P,Q两点运动到使∠PQE=60°时,求四边形PQEC的面积;
(4)是否存在某一时刻t,使PQ+QE的值最小?若存在,请求t的值,并求出此时PQ+QE的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
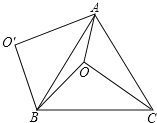
【题目】如图,O是等边△ABC内一点,OA=6,OB=8,OC=10,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO',下列结论:①△BO'A可以由△BOC绕点B逆时针旋转60°得到;②点O与O'的距离为8;③四边形AOBO'的面积为24+15![]() ; ④∠AOB=150°;⑤s△AOC+S△AOB=9
; ④∠AOB=150°;⑤s△AOC+S△AOB=9![]() +24,其中正确的结论是_____.
+24,其中正确的结论是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某品牌自行车的最新车型实物图和简化图,它在轻量化设计、刹车、车篮和座位上都做了升级.A为后胎中心,经测量车轮半径AD为30cm,中轴轴心C到地面的距离CF为30cm,座位高度最低刻度为155cm,此时车架中立管BC长为54cm,且∠BCA=71°.(参考数据:sin71°≈0.95,cos71°≈0.33,tan71°≈2.88)
(1)求车座B到地面的高度(结果精确到1cm);
(2)根据经验,当车座B'到地面的距离B'E'为90cm时,身高175cm的人骑车比较舒适,此时车架中立管BC拉长的长度BB'应是多少?(结果精确到1cm)
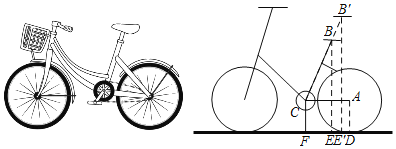
查看答案和解析>>
科目:初中数学 来源: 题型:
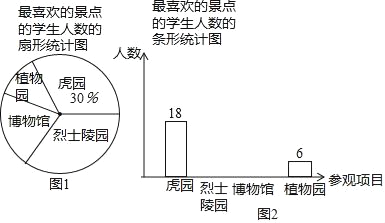
【题目】某校在一次社会实践活动中,组织学生参观了虎园、烈士陵园、博物馆和植物园,为了解本次社会实践活动的效果,学校随机抽取了部分学生,对“最喜欢的景点”进行了问卷调查,并根据统计结果绘制了如下不完整的统计图.其中最喜欢烈士陵园的学生人数与最喜欢博物馆的学生人数之比为2:1,请结合统计图解答下列问题:
(1)本次活动抽查了 名学生;
(2)请补全条形统计图;
(3)在扇形统计图中,最喜欢植物园的学生人数所对应扇形的圆心角是 度;
(4)该校此次参加社会实践活动的学生有720人,请求出最喜欢烈士陵园的人数约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】发现
如图1,在有一个“凹角∠A1A2A3”n边形A1A2A3A4……An中(n为大于3的整数),∠A1A2A3=∠A1+∠A3+∠A4+∠A5+∠A6+……+∠An﹣(n﹣4)×180°.
验证
(1)如图2,在有一个“凹角∠ABC”的四边形ABCD中,证明:∠ABC=∠A+∠C+∠D.
(2)证明3,在有一个“凹角∠ABC”的六边形ABCDEF中,证明;∠ABC=∠A+∠C+∠D+∠E+∠F﹣360°.
延伸
(3)如图4,在有两个连续“凹角A1A2A3和∠A2A3A4”的四边形A1A2A3A4……An中(n为大于4的整数),∠A1A2A3+∠A2A3A4=∠A1+∠A4+∠A5+∠A6……+∠An﹣(n﹣ )×180°.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com