
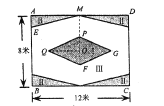
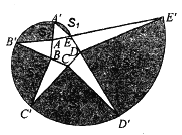
����Ŀ����ͼ��ijУ������12�ף���8�ľ���![]() ���ڳ��ؽ��е���װ�Σ��ֽ��仮��Ϊ������������
���ڳ��ؽ��е���װ�Σ��ֽ��仮��Ϊ������������![]() ������������4��ȫ�ȵ�ֱ�������Σ���ʣ��հײ��ּ�Ϊ����������
������������4��ȫ�ȵ�ֱ�������Σ���ʣ��հײ��ּ�Ϊ����������![]() Ϊ���κ����εĶԳ����ģ�
Ϊ���κ����εĶԳ����ģ�![]() ��
��![]() ��
��![]() ��Ϊ�����ۣ�Ҫ�����������������������
��Ϊ�����ۣ�Ҫ�����������������������![]() �����
�����![]() ������
������![]() ��.
��.
�� | �� | �� | |
���ۣ�Ԫ/��2�� |
|
|
|
��1����![]() ʱ���������������.
ʱ���������������.
��2���ƻ��������������ֱ�����ף������ͬ����ɫ��ש����������������ɫ��ש��
������ͬ���������£��������ڰ�ɫ��������Խ�����ڹ�������Խ��.��![]() Ϊ����ʱ�����ڹ���������ã������ʱ��ɫ��������.
Ϊ����ʱ�����ڹ���������ã������ʱ��ɫ��������.
�����ִ�ש�ĵ����б����£�![]() ��Ϊ������������
��Ϊ������������![]() ��ʱ�����������ש���ܷ������٣������ٷ���Ϊ7200Ԫ����ʱ
��ʱ�����������ש���ܷ������٣������ٷ���Ϊ7200Ԫ����ʱ![]() __________��
__________��
���𰸡���1��8m2;��2��68m2;(3) 40��8
��������
��1���������ĶԳ�ͼ�����ʺ�,![]() ,
,![]() ,
,![]() �ɵ�
�ɵ�![]() ,���ɽ
,���ɽ![]() ʱ��4��ȫ��ֱ�������ε������
ʱ��4��ȫ��ֱ�������ε������
��2����ɫ����������Ǿ��������ȥһ�����ֵ�������ֱ��ú�x�Ĵ���ʽ��ʾ�����κ��ĸ�ȫ��ֱ�������ε�������г�����x�Ľ���ʽ��ʾ��ɫ��������������ɶ���ʽ������![]() ��
��![]() ��
��![]() ������Ա�����ȡֵ��Χ���ٸ��ݶ��κ����������Լ��ɽ��
������Ա�����ȡֵ��Χ���ٸ��ݶ��κ����������Լ��ɽ��
��3�������x=2ʱ����������Լ��ú�m��n�Ĵ���ʽ��ʾ�����ã���Ϊm,n��Ϊ�����������m=40��n=8.
��1�� ��![]() Ϊ�����κ����εĶԳ����ģ�
Ϊ�����κ����εĶԳ����ģ�![]() ����
����![]()
��![]() ��
��![]() ����
����![]()
�൱![]() ʱ��
ʱ��![]() ��
��![]()
��2����![]() ��
��![]()
��![]() -
- ��
��
��![]() ��
��![]() ��
��![]()
�� �ⲻ��ʽ���
�ⲻ��ʽ���![]() ��
��
��![]() �����ͼ��
�����ͼ��![]() ʱ��
ʱ��![]() ��
��![]() ���������С.
���������С.
�൱![]() ʱ��
ʱ�� ![]() ȡ�����ֵΪ
ȡ�����ֵΪ![]()
��3���ߵ�![]() ʱ��S��=4x2=16 m2��
ʱ��S��=4x2=16 m2��![]() =12 m2��
=12 m2��![]() =68m2���ܷ���:16��2m+12��5n+68��2m=7200,����ã�5n+14m=600,��Ϊm,n��Ϊ�����������m=40��n=8.
=68m2���ܷ���:16��2m+12��5n+68��2m=7200,����ã�5n+14m=600,��Ϊm,n��Ϊ�����������m=40��n=8.


 Сѧ��ʱ��ҵȫͨ����ϵ�д�
Сѧ��ʱ��ҵȫͨ����ϵ�д� �����ÿ�ʱѵ��ϵ�д�
�����ÿ�ʱѵ��ϵ�д� ��Ԫȫ��������ϵ�д�
��Ԫȫ��������ϵ�д� �»ƸԱ����ܾ�ϵ�д�
�»ƸԱ����ܾ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣�������y��ax2+bx+c������A����2��0����B��4��0����C��0��3�����㣮
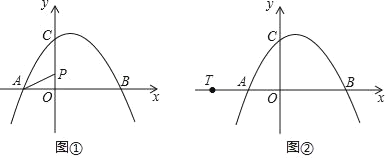
��1�����������ߵĽ���ʽ��
��2����P��y���ϵ�һ�����㣬����PA������5PA+4PC����Сֵ��
��3����ͼ�ڣ���ֱ��l������T����4��0����QΪֱ��l�ϵĶ��㣬����A��B��QΪ����������ֱ�����������ҽ�������ʱ������ֱ��l�Ľ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ���ִ����е� B ��ʱ�����С�� A �ڴ��ı�ƫ�� 60��ķ����ִ��� B ������������������ 20 ���ﵽ�� C ��ʱ�����С�� A �ڱ����ı�ƫ�� 30��ķ���
��1����С�� A �������ִ�����·�� BC �ľ����� AD���� AD �ij���
��2����֪��С����Χ 17 �������а��������ִ����ı亽�������ǰ��ʻ�������ִ���������Σ�գ���![]() ��1.732��
��1.732��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��E�dz�����ABCD�ı�AB�ϵĵ㣬EF��DE��BC�ڵ�F
��1����֤����ADE�ס�BEF��
��2����H��ED��һ�㣬��EHΪֱ������O��DF����O�����ڵ�G����DH��OH��3����ͼ����Ӱ���ֵ���������������С��������һλ��![]() ��1.73������3.14����
��1.73������3.14����
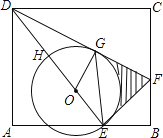
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����������![]() �Ķ���
�Ķ���![]() ΪԲ�ģ�
ΪԲ�ģ�![]() Ϊ�뾶��Բ����
Ϊ�뾶��Բ����![]() ���ӳ����ڵ�
���ӳ����ڵ�![]() �����Ե�
�����Ե�![]() ΪԲ�ģ�
ΪԲ�ģ�![]() Ϊ�뾶��Բ����
Ϊ�뾶��Բ����![]() ���ӳ�����
���ӳ�����![]() �����ν��������õ������ߣ���˳������
�����ν��������õ������ߣ���˳������![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ���õ�5����Ӱ�����������ǵ�����ֱ�Ϊ
���õ�5����Ӱ�����������ǵ�����ֱ�Ϊ![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��������
��������![]() ����
����![]() ��ֵΪ�� ��
��ֵΪ�� ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ���ų�Ա��������ѧ��֪ʶ����ij����ƵĿ���![]() ͼ���߶�MN�ij�
ͼ���߶�MN�ij�![]() ��ֱ��MN��ֱ�ڵ��棬����Ϊ��
��ֱ��MN��ֱ�ڵ��棬����Ϊ��![]() �ڵ���A����õ�M������Ϊ
�ڵ���A����õ�M������Ϊ![]() ����N������Ϊ
����N������Ϊ![]() ����B����õ�M������Ϊ
����B����õ�M������Ϊ![]() ��
��![]() �ף���A��B��P������һֱ����
�ף���A��B��P������һֱ����![]() ������������������ƵĿ�MN�ij���
������������������ƵĿ�MN�ij���
![]() �ο����ݣ�
�ο����ݣ�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]()

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
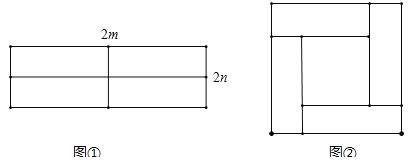
����Ŀ����ͼ��ͼ����ʾ��һ����Ϊ2m����Ϊ2n�ij����Σ��ü������ֳ��ĸ�С�����Σ�Ȼ��ͼ�ڵķ�ʽƴ��һ���������Σ�
��1��ͼ���еĴ������εı߳������� ����ͼ���е�С�����εı߳������� ����
��2��ͼ���еĴ������ε���������� ����ͼ���е�С�����ε���������� ����ͼ����ÿ��С�����ε�������� ����
��3���۲�ͼ�ڣ�����д����m+n��2����m��n��2��mn����������ʽ��ĵ�����ϵ���� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У���E��F�ֱ�����BC��CD���˶����������EAF��45�㣬AE��AF�ֱ���BD�ཻ�ڵ�M��N������˵���У���BE+DF��EF������A���߶�EF�ľ���һ�����������εı߳�������tan��BAE��![]() ����tan��DAF��
����tan��DAF��![]() ������BE��2��DF��3����S��AEF��18�����н�����ȷ����__������ȷ�����д�ں����ϣ�
������BE��2��DF��3����S��AEF��18�����н�����ȷ����__������ȷ�����д�ں����ϣ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com