
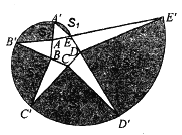
【题目】如图,以正五边形![]() 的顶点
的顶点![]() 为圆心,
为圆心,![]() 为半径作圆弧交
为半径作圆弧交![]() 的延长线于点
的延长线于点![]() ,再以点
,再以点![]() 为圆心,
为圆心,![]() 为半径作圆弧交
为半径作圆弧交![]() 的延长线于
的延长线于![]() ,依次进行……得到螺旋线,再顺次连结
,依次进行……得到螺旋线,再顺次连结![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,得到5块阴影区域,若记它们的面积分别为
,得到5块阴影区域,若记它们的面积分别为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,且满足
,且满足![]() ,则
,则![]() 的值为( )
的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
由题意得,五个扇形的圆心角相等,所以面积比是半径比的平方,根据面积比可表示出五个扇形面积,再根据底相等的三角形面积比等于高的比求出五个三角形的面积比并表示出来,从而分别求出各个阴影部分的面积,再根据![]() 即可求解.
即可求解.
解:因为扇形AEA′、扇形BB′A′、扇形CC′B′、扇形DD′C′、扇形EE′D′圆心角相等,都是72°,半径分别是正五边形半径、半径的二倍、三倍、四倍、五倍,
由扇形面积公式可得,五个扇形面积从小到大的比是1:4:9:16:25,设:扇形AEA′的面积=m,则扇形BB′A′、扇形CC′B′、扇形DD′C′、扇形EE′D′的面积依次为:4m、9m、16m、25m;△AEA′、△BB′A′、△CC′B′、△DD′C′、△EE′D′中,AE=AB=BC=CD=DE,AA′:BB′:CC′:DD′:EE′=1:2:3:4:5,五个三角形分别以AE、AB、BC、CD、DE为底,易证五个三角形的面积比依次为:1:2:3:4:5,设S△AEA′=n,
则S△BB′A′=2n、S△CC′B′=3n、S△DD′C′=4n、S△EE′D′=5n,所以S5=25m-5n , S2=4m-2n , S4=16m-4n , S3=9m-3n , 因为![]() ,所以(25m-5n)-(4m-2n)=1,解得:7m-n=
,所以(25m-5n)-(4m-2n)=1,解得:7m-n=![]() ,所以
,所以![]() =(16m-4n)-(9m-3n)=7m-n=
=(16m-4n)-(9m-3n)=7m-n=![]() .
.
故选:D.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:
【题目】现如今,“垃圾分类”意识已深入人心,垃圾一般可分为:可回收物、厨余垃圾、有害垃圾、其它垃圾.其中甲拿了一袋垃圾,乙拿了两袋垃圾.
(1)直接写出甲所拿的垃圾恰好是“厨余垃圾”的概率;
(2)求乙所拿的两袋垃圾不同类的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形ABCD中,E是对角线AC上的一个动点,连结BE并延长交直线AD于点F.
(1)若AB=10,sin∠BAC=![]() ;
;
①求对角线AC的长;
②若BE=4![]() ,求AE的长;
,求AE的长;
(2)若点F在边AD上,且![]() =k,△BEC和四边形ECDF的面积分别是S1和S2,求
=k,△BEC和四边形ECDF的面积分别是S1和S2,求![]() 的最大值.
的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,AB=OB=8,∠ABO=90°,∠yOC=45°,射线OC以每秒2个单位长度的速度向右平行移动,当射线OC经过点B时停止运动,设平行移动x秒后,射线OC扫过Rt△ABO的面积为y.
(1)求y与x之间的函数关系式;
(2)当x=3秒时,射线OC平行移动到O′C′,与OA相交于G,如图2,求经过G,O,B三点的抛物线的解析式;
(3)现有一动点P在(2)中的抛物线上,试问点P在运动过程中,是否存在△POB的面积S=8的情况?若存在,求出点P的坐标,若不存在,请说明理由.
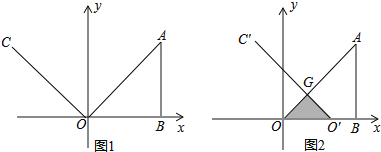
查看答案和解析>>
科目:初中数学 来源: 题型:
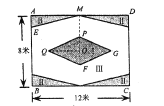
【题目】如图,某校准备给长12米,宽8米的矩形![]() 室内场地进行地面装饰,现将其划分为区域Ⅰ(菱形
室内场地进行地面装饰,现将其划分为区域Ⅰ(菱形![]() ),区域Ⅱ(4个全等的直角三角形),剩余空白部分记为区域Ⅲ;点
),区域Ⅱ(4个全等的直角三角形),剩余空白部分记为区域Ⅲ;点![]() 为矩形和菱形的对称中心,
为矩形和菱形的对称中心,![]() ,
,![]() ,
,![]() ,为了美观,要求区域Ⅱ的面积不超过矩形
,为了美观,要求区域Ⅱ的面积不超过矩形![]() 面积的
面积的![]() ,若设
,若设![]() 米.
米.
甲 | 乙 | 丙 | |
单价(元/米2) |
|
|
|
(1)当![]() 时,求区域Ⅱ的面积.
时,求区域Ⅱ的面积.
(2)计划在区域Ⅰ,Ⅱ分别铺设甲,乙两款不同的深色瓷砖,区域Ⅲ铺设丙款白色瓷砖,
①在相同光照条件下,当场地内白色区域的面积越大,室内光线亮度越好.当![]() 为多少时,室内光线亮度最好,并求此时白色区域的面积.
为多少时,室内光线亮度最好,并求此时白色区域的面积.
②三种瓷砖的单价列表如下,![]() 均为正整数,若当
均为正整数,若当![]() 米时,购买三款瓷砖的总费用最少,且最少费用为7200元,此时
米时,购买三款瓷砖的总费用最少,且最少费用为7200元,此时![]() __________,
__________,
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明参加某个智力竞答节目,答对最后两道单选题就顺利通关.第一道单选题有3个选项,第二道单选题有4个选项,这两道题小明都不会,不过小明还有一个“求助”没有用(使用“求助”可以让主持人去掉其中一题的一个错误选项).
(1)如果小明第一题不使用“求助”,那么小明答对第一道题的概率是 .
(2)如果小明将“求助”留在第二题使用,请用树状图或者列表来分析小明顺利通关的概率.
(3)从概率的角度分析,你建议小明在第几题使用“求助”.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
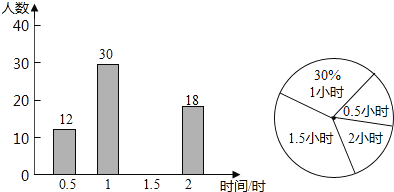
【题目】为了提高学生阅读能力,我区某校倡议八年级学生利用双休日加强课外阅读,为了解同学们阅读的情况,学校随机抽查了部分同学周末阅读时间,并且得到数据绘制了不完整的统计图,根据图中信息回答下列问题:
(1)将条形统计图补充完整;被调查的学生周末阅读时间众数是多少小时,中位数是多少小时;
(2)计算被调查学生阅读时间的平均数;
(3)该校八年级共有500人,试估计周末阅读时间不低于1.5小时的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
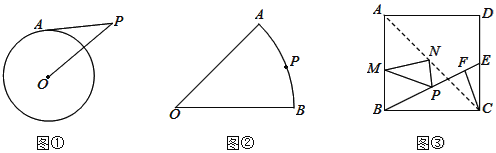
【题目】解决问题:
![]() 如图
如图![]() ,半径为4的
,半径为4的![]() 外有一点P,且
外有一点P,且![]() ,点A在
,点A在![]() 上,则PA的最大值和最小值分别是______和______.
上,则PA的最大值和最小值分别是______和______.
![]() 如图
如图![]() ,扇形AOB的半径为4,
,扇形AOB的半径为4,![]() ,P为弧AB上一点,分别在OA边找点E,在OB边上找一点F,使得
,P为弧AB上一点,分别在OA边找点E,在OB边上找一点F,使得![]() 周长的最小,请在图
周长的最小,请在图![]() 中确定点E、F的位置并直接写出
中确定点E、F的位置并直接写出![]() 周长的最小值;
周长的最小值;
拓展应用
![]() 如图
如图![]() ,正方形ABCD的边长为
,正方形ABCD的边长为![]() ;E是CD上一点
;E是CD上一点![]() 不与D、C重合
不与D、C重合![]() ,
,![]() 于F,P在BE上,且
于F,P在BE上,且![]() ,M、N分别是AB、AC上动点,求
,M、N分别是AB、AC上动点,求![]() 周长的最小值.
周长的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com