
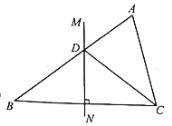
【题目】如图,在△ABC中,BC的垂直平分线MN交AB于点D,CD平分∠ACB.若AD=2,BD=3,则AC的长为_____.
【答案】![]()
【解析】
作AM⊥BC于E,由角平分线的性质得出![]() ,设AC=2x,则BC=3x,由线段垂直平分线得出MN⊥BC,BN=CN=
,设AC=2x,则BC=3x,由线段垂直平分线得出MN⊥BC,BN=CN=![]() x,得出MN∥AE,得出
x,得出MN∥AE,得出![]() ,NE=x,BE=BN+EN=
,NE=x,BE=BN+EN=![]() x,CE=CNEN=
x,CE=CNEN=![]() x,再由勾股定理得出方程,解方程即可得出结果.
x,再由勾股定理得出方程,解方程即可得出结果.
解:作AM⊥BC于E,如图所示:
∵CD平分∠ACB,
∴![]() ,
,
设AC=2x,则BC=3x,
∵MN是BC的垂直平分线,
∴MN⊥BC,BN=CN=![]() x,
x,
∴MN∥AE,
∴![]() ,
,
∴NE=x,
∴BE=BN+EN=![]() x,CE=CNEN=
x,CE=CNEN=![]() x,
x,
由勾股定理得:AE2=AB2BE2=AC2CE2,
即52(![]() x)2=(2x)2(
x)2=(2x)2(![]() x)2,
x)2,
解得:x=![]() ,
,
∴AC=2x=![]() ;
;
故答案为![]() .
.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:
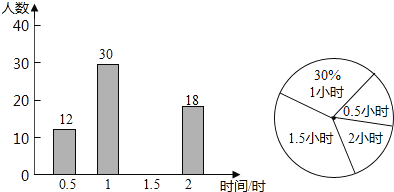
【题目】为了提高学生阅读能力,我区某校倡议八年级学生利用双休日加强课外阅读,为了解同学们阅读的情况,学校随机抽查了部分同学周末阅读时间,并且得到数据绘制了不完整的统计图,根据图中信息回答下列问题:
(1)将条形统计图补充完整;被调查的学生周末阅读时间众数是多少小时,中位数是多少小时;
(2)计算被调查学生阅读时间的平均数;
(3)该校八年级共有500人,试估计周末阅读时间不低于1.5小时的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
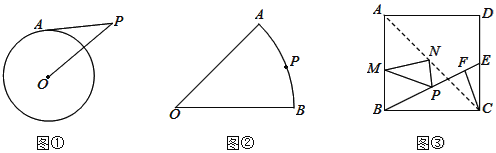
【题目】解决问题:
![]() 如图
如图![]() ,半径为4的
,半径为4的![]() 外有一点P,且
外有一点P,且![]() ,点A在
,点A在![]() 上,则PA的最大值和最小值分别是______和______.
上,则PA的最大值和最小值分别是______和______.
![]() 如图
如图![]() ,扇形AOB的半径为4,
,扇形AOB的半径为4,![]() ,P为弧AB上一点,分别在OA边找点E,在OB边上找一点F,使得
,P为弧AB上一点,分别在OA边找点E,在OB边上找一点F,使得![]() 周长的最小,请在图
周长的最小,请在图![]() 中确定点E、F的位置并直接写出
中确定点E、F的位置并直接写出![]() 周长的最小值;
周长的最小值;
拓展应用
![]() 如图
如图![]() ,正方形ABCD的边长为
,正方形ABCD的边长为![]() ;E是CD上一点
;E是CD上一点![]() 不与D、C重合
不与D、C重合![]() ,
,![]() 于F,P在BE上,且
于F,P在BE上,且![]() ,M、N分别是AB、AC上动点,求
,M、N分别是AB、AC上动点,求![]() 周长的最小值.
周长的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】十八大报告首次提出建设生态文明,建设美丽中国.十九大报告再次明确,到2035年美丽中国目标基本实现.森林是人类生存发展的重要生态保障,提高森林的数量和质量对生态文明建设非常关键.截止到2013年,我国已经进行了八次森林资源清查,其中全国和北京的森林面积和森林覆盖率情况如下:
表1全国森林面积和森林覆盖率
清查次数 | 一 (1976年) | 二 (1981年) | 三 (1988年) | 四 (1993年) | 五 (1998年) | 六 (2003年) | 七 (2008年) | 八 (2013年) |
森林面积(万公顷) | 12200 | 1150 | 12500 | 13400 | 15894. 09 | 17490.92 | 19545.22 | 20768.73 |
森林覆盖率 | 12.7% | 12% | 12.98% | 13.92% | 16.55% | 18.21% | 20.36% | 21.63% |
表2北京森林面积和森林覆盖率
清查次数 | 一 (1976年) | 二 (1981年) | 三 (1988年) | 四 (1993年) | 五 (1998年) | 六 (2003年) | 七 (2008年) | 八 (2013年) |
森林面积(万公顷) | 33.74 | 37.88 | 52.05 | 58.81 | ||||
森林覆盖率 | 11.2% | 8.1% | 12.08% | 14.99% | 18.93% | 21.26% | 31.72% | 35.84% |
(以上数据来源于中国林业网)
请根据以上信息解答下列问题:
(1)从第 次清查开始,北京的森林覆盖率超过全国的森林覆盖率;
(2)补全以下北京森林覆盖率折线统计图,并在图中标明相应数据;

(3)第八次清查的全国森林面积20768.73(万公顷)记为a,全国森林覆盖率21.63%记为b,到2018年第九次森林资源清查时,如果全国森林覆盖率达到27.15%,那么全国森林面积可以达到 万公顷(用含a和b的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
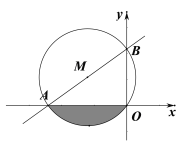
【题目】一次函数![]() 的图像与x轴的负半轴相交于点A,与y轴的正半轴相交于点B,且
的图像与x轴的负半轴相交于点A,与y轴的正半轴相交于点B,且![]() △OAB的外接圆的圆心M的横坐标为-3.
△OAB的外接圆的圆心M的横坐标为-3.
(1)求一次函数的解析式;
(2)求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】□ABCD中,E、F是对角线BD上不同的两点,下列条件中,不能得出四边形AECF一定为平行四边形的是( )
A. BE=DF B. AE=CF C. AF//CE D. ∠BAE=∠DCF
查看答案和解析>>
科目:初中数学 来源: 题型:
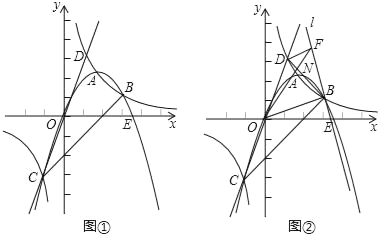
【题目】如图①,双曲线y=![]() (k≠0)和抛物线y=ax2+bx(a≠0)交于A、B、C三点,其中B(3,1),C(﹣1,﹣3),直线CO交双曲线于另一点D,抛物线与x轴交于另一点E.
(k≠0)和抛物线y=ax2+bx(a≠0)交于A、B、C三点,其中B(3,1),C(﹣1,﹣3),直线CO交双曲线于另一点D,抛物线与x轴交于另一点E.
(1)求双曲线和抛物线的解析式;
(2)抛物线在第一象限部分是否存在点P,使得∠POE+∠BCD=90°?若存在,请求出满足条件的点P的坐标;若不存在,请说明理由;
(3)如图②,过B作直线l⊥OB,过点D作DF⊥l于点F,BD与OF交于点N,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=5cm,BD=8cm,动点P从点B开始沿BC边匀速运动,动点Q从点D开始沿对角线DB匀速运动,它们的运动速度均为1cm/s,过点Q作QE⊥CD,与CD交于点E,连接PQ,点P和点Q同时出发,设运动时间为t(s),0<t≤5.
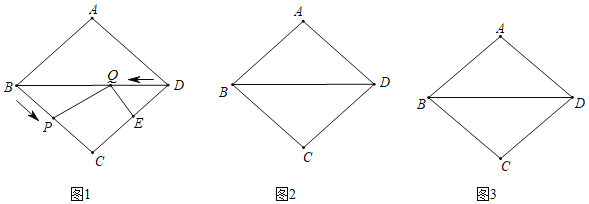
(1)当PQ∥CD时,求t的值;
(2)设四边形PQEC的面积为S(cm2),求S与t之间的函数关系式;
(3)当P,Q两点运动到使∠PQE=60°时,求四边形PQEC的面积;
(4)是否存在某一时刻t,使PQ+QE的值最小?若存在,请求t的值,并求出此时PQ+QE的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD的边长AB=2,E为AB的中点,F为BC的中点,AF分别与DE、BD相交于点M,N,则MN的长为( )
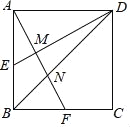
A. ![]() B.
B. ![]() ﹣1 C.
﹣1 C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com