
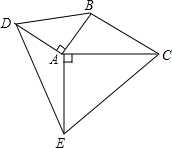
 如图,在△ABC中,AB=2,BC=3,AC=4,△ABD和△ACE均为等腰直角三角形,则DE=
如图,在△ABC中,AB=2,BC=3,AC=4,△ABD和△ACE均为等腰直角三角形,则DE=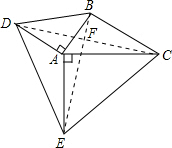 解:如图,连接BE、CD,BE与CD于F.
解:如图,连接BE、CD,BE与CD于F.
|
| 2 |
| 2 |
| 31 |
| 31 |


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案科目:初中数学 来源: 题型:
 如图所示,在⊙O上取A、B两个点,测量出小于半圆的弧即
如图所示,在⊙O上取A、B两个点,测量出小于半圆的弧即 |
| AB |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减/辆 | -1 | +3 | -2 | +4 | +7 | -5 | -10 |
查看答案和解析>>
科目:初中数学 来源: 题型:
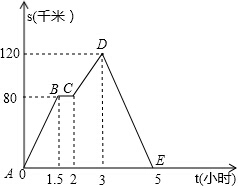 如图折线ABCDE描述了一汽车在某一直路上行驶时汽车离出发地的距离s(千米)和行驶时间t(小时)间的变量关系,则下列结论正确的是( )
如图折线ABCDE描述了一汽车在某一直路上行驶时汽车离出发地的距离s(千米)和行驶时间t(小时)间的变量关系,则下列结论正确的是( )| A、汽车共行驶了120千米 |
| B、汽车在行驶途中停留了2小时 |
| C、汽车在整个行驶过程中的平均速度为每小时24千米 |
| D、汽车自出发后3小时至5小时间行驶的速度为每小时60千米 |
查看答案和解析>>
科目:初中数学 来源: 题型:
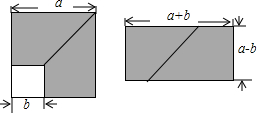 如图的分割正方形,拼接成长方形方案中,可以验证( )
如图的分割正方形,拼接成长方形方案中,可以验证( )| A、(a+b)2=a2+2ab+b2 |
| B、(a-b)2=a2-2ab+b2 |
| C、(a+b)2=(a+b)2-4ab |
| D、(a+b)(a-b)=a2-b2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com