
【题目】如图(1),将两块直角三角板的直角顶点C叠放在一起.
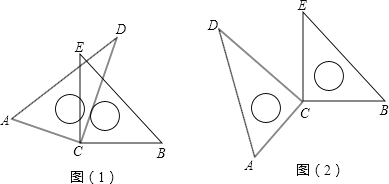
(1)试判断∠ACE与∠BCD的大小关系,并说明理由;
(2)若∠DCE=30°,求∠ACB的度数;
(3)猜想∠ACB与∠DCE的数量关系,并说明理由;
(4)若改变其中一个三角板的位置,如图(2),则第(3)小题的结论还成立吗?(不需说明理由)
【答案】(1)∠ACE=∠BCD;(2)150°;(3)∠ECD+∠ACB=180°;(4)成立.
【解析】解:(1)∠ACE=∠BCD,理由如下:
∵∠ACD=∠BCE=90°,∠ACE+∠ECD=∠ECB+∠ECD=90°,
∴∠ACE=∠BCD;
(2)若∠DCE=30°,∠ACD=90°,
∴∠ACE=∠ACD﹣∠DCE=90°﹣30°=60°,
∵∠BCE=90°且∠ACB=∠ACE+∠BCE,
∠ACB=90°+60°=150°;
(3)猜想∠ACB+∠DCE=180°.理由如下:
∵∠ACD=90°=∠ECB,∠ACD+∠ECB+∠ACB+∠DCE=360°,
∴∠ECD+∠ACB=360°﹣(∠ACD+∠ECB)=360°﹣180°=180°;
(4)成立.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案科目:初中数学 来源: 题型:
【题目】要得到y=(x-3)2-2的图象,只要将y=x2的图象
A. 由向左平移3个单位,再向上平移2个单位;
B. 由向右平移3个单位,再向下平移2个单位;
C. 由向右平移3个单位,再向上平移2个单位;
D. 由向左平移3个单位,再向下平移2个单位.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一块直角三角形纸片,两直角边分别为:AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,求CD的长。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.请将解题过程填写完整.

解:∵EF∥AD(已知)
∴∠2=∠3 )---①
又∵∠1=∠2(已知)
∴∠1=∠3( )----②
∴AB∥______( )----③
∴∠BAC+∠AGD=180°( )----④
∵∠BAC=70°(已知)
∴∠AGD=1800-700=1100
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】海水受日月的引力而产生潮汐现象.早晨海水上涨叫做潮,黄昏海水上涨叫做汐,合称潮汐.潮汐与人类的生活有着密切的联系.某港口某天从0时到12时的水深情况如下表,其中T表示时刻,h表示水深.
T(时) | 0 | 3 | 6 | 9 | 12 |
h(米) | 5 | 7.4 | 5.1 | 2.6 | 4.5 |
上述问题中,字母T,h表示的是变量还是常量,简述你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如表是某报纸公布的世界人口数据情况:
年份 | 1957 | 1974 | 1987 | 1999 | 2010 | 2025 |
人口数 | 30亿 | 40亿 | 50亿 | 60亿 | 70亿 | 80亿 |
(1)表中有几个变量?
(2)如果要用x表示年份,用y表示世界人口总数,那么随着x的变化,y的变化趋势是怎样的?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某九年级制学校围绕“每天30分钟的大课间,你最喜欢的体育活动项目是什么?(只写一项)”的问题,对在校学生进行随机抽样调查,从而得到一组数据.图1是根据这组数据绘制的条形统计图,请结合统计图回答下列问题:

(1)该校对多少学生进行了抽样调查?
(2)本次抽样调查中,最喜欢篮球活动的有多少?占被调查人数的百分比是多少?
(3)若该校九年级共有200名学生,图2是根据各年级学生人数占全校学生总人数的百分比绘制的扇形统计图,请你估计全校学生中最喜欢跳绳活动的人数约为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com