
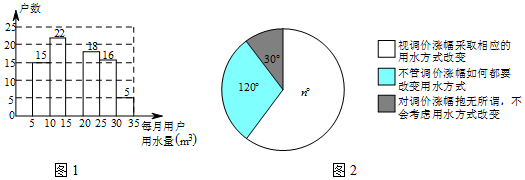
分析 (1)首先根据圆周角等于360°,求出的值是多少即可;然后用“视水价格调价涨幅抱无所谓态度”的居民的户数除以它占被调查的居民户数的分率,求出小明调查了多少户居民;最后求出每月每户的用水量在15m3-20m3之间的居民的户数,补全图1即可.
(2)根据中位数的含义分别进行解答即可.
(3)根据分数乘法的意义,用小明所在小区居民的户数乘以“视调价涨幅采取相应的用水方式改变”的居民户数占被调查的居民户数的分率,求出“视调价涨幅采取相应的用水方式改变”的居民户数有多少即可.
解答 解:(1)n=360-30-120=210,
∵8÷$\frac{30}{360}$=96(户)
∴小明调查了96户居民.
每月每户的用水量在15m3-20m3之间的居民的户数是:
96-(15+22+18+16+5)
=96-76
=20(户).
(2)96÷2=48(户),15+12=37(户),15+22+20=57(户),
∵每月每户的用水量在5m3-15m3之间的有37户,每月每户的用水量在5m3-20m3之间的有57户,
∴把每月每户用水量这组数据从小到大排列后,第48个、第49个数在15-20之间,
∴第48个、第49个数的平均数也在15-20之间,
∴每月每户用水量的中位数落在15-20之间.
(3)∵1200×$\frac{210}{360}$=700(户),
答:视调价涨幅采取相应的用水方式改变”的居民户数有700户.
点评 此题主要考查了对条形统计图的认识和了解,要善于从条形统计图中获取信息,并能利用获取的信息解决实际问题.还考查了用样本估计总体,解答此题的关键是要明确众数的含义以及求法.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 篮球场上,小金、小木、小火、小水、小土五人打算先选出一人做裁判,然后将其余四人组成两队打比赛,选人规则如下:五人都伸出右脚,让五个脚尖围在一起成“圆圈”状,其中一人将球从“圆圈”的中心处向上竖直抛起,球落到地面上弹起、落下如此反复,直到停止运动,在此过程中,篮球碰到谁的脚尖,谁就将脚收回,直到剩下两人时,选人结束,第一个收回脚的是裁判,第二、三个收回脚的为一队,剩下的两人为另一队,若截止到球停止运动时碰到的脚尖小于三个,则重新考试.前按此规则,思考下面问题并回答:
篮球场上,小金、小木、小火、小水、小土五人打算先选出一人做裁判,然后将其余四人组成两队打比赛,选人规则如下:五人都伸出右脚,让五个脚尖围在一起成“圆圈”状,其中一人将球从“圆圈”的中心处向上竖直抛起,球落到地面上弹起、落下如此反复,直到停止运动,在此过程中,篮球碰到谁的脚尖,谁就将脚收回,直到剩下两人时,选人结束,第一个收回脚的是裁判,第二、三个收回脚的为一队,剩下的两人为另一队,若截止到球停止运动时碰到的脚尖小于三个,则重新考试.前按此规则,思考下面问题并回答:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m<0 | B. | 0<m≤1 | C. | 1<m<2 | D. | 1<m≤2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 鈤 |
| 与计划量的差值 | +4 | -3 | -5 | +14 | -8 | +21 | -6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com