
| A. | 对角线相等的平行四边形是矩形 | |
| B. | 对角线互相垂直的四边形是菱形 | |
| C. | 三角形的中位线平行于第三边且等于第三边的一半 | |
| D. | 三角形的一条中线能将三角形分成面积相等的两部分 |
分析 根据矩形的判定方法对A矩形判断;根据菱形的判定方法对B矩形判断;根据三角形中位线性质对C矩形判断;根据三角形中线定义和三角形面积公式对D矩形判断.
解答 解:A、对角线相等的平行四边形是矩形,所以A选项为真命题;
B、对角线互相垂直的平行四边形是菱形,所以B选项为假命题;
C、三角形的中位线平行于第三边且等于第三边的一半,所以C选项为真命题;
D、三角形的一条中线能将三角形分成面积相等的两部分,所以D选项为真命题.
故选B.
点评 本题考查了命题与定理:判断一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,一个命题可以写成“如果…那么…”形式. 有些命题的正确性是用推理证实的,这样的真命题叫做定理.


 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:填空题
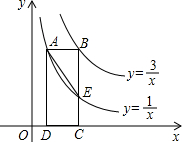 如图,矩形ABCD的一边CD在x轴上,顶点A、B分别落在双曲线y=$\frac{1}{x}$(x>0)、y=$\frac{3}{x}$(x>0)上,边BC交双曲线y=$\frac{1}{x}$(x>0)于点E,连接AE,则△ABE的面积为$\frac{2}{3}$.
如图,矩形ABCD的一边CD在x轴上,顶点A、B分别落在双曲线y=$\frac{1}{x}$(x>0)、y=$\frac{3}{x}$(x>0)上,边BC交双曲线y=$\frac{1}{x}$(x>0)于点E,连接AE,则△ABE的面积为$\frac{2}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
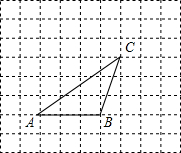 在正方形网格中,△ABC的位置如图所示,则sin∠BAC的值为( )
在正方形网格中,△ABC的位置如图所示,则sin∠BAC的值为( )| A. | $\frac{3}{5}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{5}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
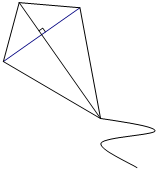 如图,小明将一根长为1.4米的竹条截为两段,并互相垂直固定,作为风筝的龙骨,制作成了一个面积为0.24米2的风筝.请你计算一下将竹条截成长度分别为多少的两段?
如图,小明将一根长为1.4米的竹条截为两段,并互相垂直固定,作为风筝的龙骨,制作成了一个面积为0.24米2的风筝.请你计算一下将竹条截成长度分别为多少的两段?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
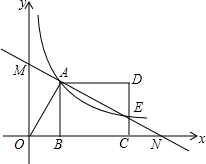 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过线段OA的端点A,O为原点,作AB⊥x轴于点B,点B的坐标为(2,0),tan∠AOB=$\frac{3}{2}$.
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过线段OA的端点A,O为原点,作AB⊥x轴于点B,点B的坐标为(2,0),tan∠AOB=$\frac{3}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
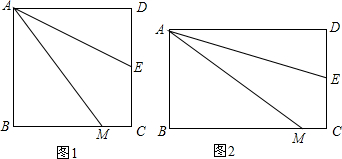
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
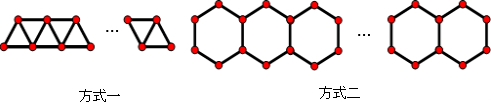
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
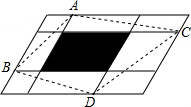 如图,在一个平行四边形中,两对平行于边的直线将这个平行四边形分为九个小平行四边形,如果原来这个平行四边形的面积为100cm2,而中间那个小平行四边形(阴影部分)的面积为20平方厘米,则四边形ABDC的面积是60cm2.
如图,在一个平行四边形中,两对平行于边的直线将这个平行四边形分为九个小平行四边形,如果原来这个平行四边形的面积为100cm2,而中间那个小平行四边形(阴影部分)的面积为20平方厘米,则四边形ABDC的面积是60cm2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com