
【题目】综合题
(1)如图①,若∠B+∠D=∠BED,试猜想AB与CD的位置关系,并说明理由。
(2)如图②,要想得到AB∥CD,则∠1、∠2、∠3之间应满足怎样的位置关系?请探索。
【答案】
(1)解:AB∥CD.在∠BED的内部作∠BEF=∠B, ∴AB∥EF. ∵∠B+∠D=∠BED,∴∠BE F+∠FED=∠BED, ∴∠FED=∠D, ∴EF∥CD, ∴A B∥CD
(2)解:延长EA交CD于点F,∴∠AFD=∠2+∠3 ,要想得到AB∥CD,则满足∠1=∠AFD ,故要想得到AB∥CD,则∠1、∠2、∠3之间应满足∠1=∠2+∠3即可。
【解析】(1)AB∥CD.在∠BED的内部作∠BEF=∠B ,根据内错角相等二直线平行得出AB∥EF ,因∠B+∠D=∠BED, ∠BE F+∠FED=∠BED, 故∠FED=∠D,根据内错角相等二直线平行得出EF∥CD,根据平行于同一直线的两条直线平行得出A B∥CD ;
根据三角形的外角和定理及平行线的判定方法即可得出∠1=∠2+∠3 。


科目:初中数学 来源: 题型:
【题目】阅读下面材料:
小明遇到这样一个问题:如图1,△ABC中,AB=AC,点D在BC边上,∠DAB=∠ABD,BE⊥AD,垂足为E,求证:BC=2AE.
小明经探究发现,过点A作AF⊥BC,垂足为F,得到∠AFB=∠BEA,从而可证△ABF≌△BAE(如图2),使问题得到解决.
(1)根据阅读材料回答:△ABF与△BAE全等的条件是 AAS(填“SSS”、“SAS”、“ASA”、“AAS”或“HL”中的一个)
参考小明思考问题的方法,解答下列问题:
(2)如图3,△ABC中,AB=AC,∠BAC=90°,D为BC的中点,E为DC的中点,点F在AC的延长线上,且∠CDF=∠EAC,若CF=2,求AB的长;
(3)如图4,△ABC中,AB=AC,∠BAC=120°,点D、E分别在AB、AC边上,且AD=kDB(其中0<k<![]() ),∠AED=∠BCD,求
),∠AED=∠BCD,求![]() 的值(用含k的式子表示).
的值(用含k的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 与
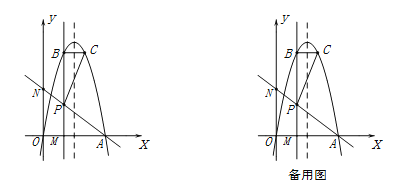
与![]() 轴相交于O、A两点(其中O为坐标原点),过点P(2,2a)作直线PM⊥x轴于点M,交抛物线于点B,点B关于抛物线对称轴的对称点为C(其中B、C不重合),连接AP交y轴于点N,连接BC和PC.
轴相交于O、A两点(其中O为坐标原点),过点P(2,2a)作直线PM⊥x轴于点M,交抛物线于点B,点B关于抛物线对称轴的对称点为C(其中B、C不重合),连接AP交y轴于点N,连接BC和PC.
(1)![]() 时,求抛物线的解析式和BC的长;
时,求抛物线的解析式和BC的长;
(2)如图![]() 时,若AP⊥PC,求
时,若AP⊥PC,求![]() 的值;
的值;
(3)是否存在实数![]() ,使
,使![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com