
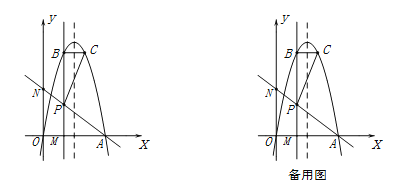
【题目】抛物线![]() 与
与![]() 轴相交于O、A两点(其中O为坐标原点),过点P(2,2a)作直线PM⊥x轴于点M,交抛物线于点B,点B关于抛物线对称轴的对称点为C(其中B、C不重合),连接AP交y轴于点N,连接BC和PC.
轴相交于O、A两点(其中O为坐标原点),过点P(2,2a)作直线PM⊥x轴于点M,交抛物线于点B,点B关于抛物线对称轴的对称点为C(其中B、C不重合),连接AP交y轴于点N,连接BC和PC.
(1)![]() 时,求抛物线的解析式和BC的长;
时,求抛物线的解析式和BC的长;
(2)如图![]() 时,若AP⊥PC,求
时,若AP⊥PC,求![]() 的值;
的值;
(3)是否存在实数![]() ,使
,使![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)![]() ,BC=2;(2)
,BC=2;(2)![]() ;(3)
;(3)![]() ..
..
【解析】
试题分析:(1)由抛物线![]() 与
与![]() 轴相交于O、A两点(其中O为坐标原点),得到b=0,故抛物线为
轴相交于O、A两点(其中O为坐标原点),得到b=0,故抛物线为![]() ,把
,把![]() 代入,得到P(2,3)和
代入,得到P(2,3)和![]() ,由对称轴x=2,即可得到BC的长;
,由对称轴x=2,即可得到BC的长;
(2)把x=2代入![]() ,得到B(2,
,得到B(2,![]() ),设C(x,
),设C(x, ![]() ),由对称轴
),由对称轴![]() ,得到C(
,得到C(![]() ,
, ![]() ),由
),由![]() ,得到A(4a,0),由AP⊥PC,得到
,得到A(4a,0),由AP⊥PC,得到![]() ,即
,即![]() ,解方程即可得到结论;
,解方程即可得到结论;
(3)由OA=4a, OM=2,得到AM=4a-2,由PM∥ON ,得到![]() , 即
, 即![]() ,解方程即可得到结论.
,解方程即可得到结论.
试题解析:(1)∵抛物线![]() 与
与![]() 轴相交于O、A两点(其中O为坐标原点),∴b=0,∴
轴相交于O、A两点(其中O为坐标原点),∴b=0,∴![]() ,当
,当![]() 时,P(2,3),
时,P(2,3),![]() ,∴
,∴![]() =
=![]() ,∴对称轴为:x=2,∴BC=2×(3-2)=2;
,∴对称轴为:x=2,∴BC=2×(3-2)=2;
(2)当x=2时,![]() =
=![]() ,∴B(2,
,∴B(2,![]() ),设C(x,
),设C(x, ![]() ),∵对称轴
),∵对称轴![]() ,∴
,∴![]() ,∴
,∴![]() ,∴C(
,∴C(![]() ,
, ![]() ),∵
),∵![]() ,∴A(4a,0),∵AP⊥PC,∴
,∴A(4a,0),∵AP⊥PC,∴![]() ,∴
,∴![]() ,整理得:
,整理得:![]() ,解得:
,解得:![]() ,∵
,∵![]() ,∴
,∴![]() ;
;
(3)∵A(4a,0),∴OA=4a,∵P(2,2a),∴OM=2,∴AM=4a-2,∵PM∥ON,∴![]() , ∴
, ∴![]() ,解得:
,解得:![]() .
.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
【题目】综合题
(1)如图①,若∠B+∠D=∠BED,试猜想AB与CD的位置关系,并说明理由。
(2)如图②,要想得到AB∥CD,则∠1、∠2、∠3之间应满足怎样的位置关系?请探索。
查看答案和解析>>
科目:初中数学 来源: 题型:
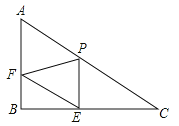
【题目】已知Rt△ABC中,∠B=90°,AC=20,AB=10,P是边AC上一点(不包括端点A、C),过点P作PE⊥BC于点E,过点E作EF∥AC,交AB于点F.设PC=x,PE=y.
(1)求y与x的函数关系式;
(2)是否存在点P使△PEF是Rt△?若存在,求此时的x的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列结论正确的有( )个:
① 规定了原点,正方向和单位长度的直线叫数轴 ② 最小的整数是0 ③ 正数,负数和零统称有理数 ④ 数轴上的点都表示有理数
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,直线BD分别交射线AE、CF于点B、D,连接A、D和B、C,∠1+∠2=180°,∠A=∠C,AD平分∠BDF,求证: 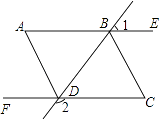
(1)AD∥BC;
(2)BC平分∠DBE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC的底边BC长为4,面积是12,腰AB的垂直平分线EF分别交AB,AC于点E、F,若点D为底边BC的中点,点M为线段EF上一动点,则△BDM的周长的最小值为 . 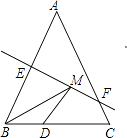
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com