
【题目】已知:如图,直线BD分别交射线AE、CF于点B、D,连接A、D和B、C,∠1+∠2=180°,∠A=∠C,AD平分∠BDF,求证: 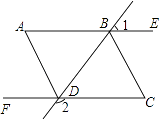
(1)AD∥BC;
(2)BC平分∠DBE.
【答案】
(1)证明:∵∠2+∠BDC=180°,∠1+∠2=180°,
∴∠1=∠DBC,
∴AB∥CF,
∴∠C=∠EBC,
∵∠A=∠C,
∴∠A=∠EBC,
∴AD∥BC;
(2)证明:∵AD平分∠BDF,
∴∠FDA=∠ADB,
∵AD∥BC,
∴∠FDA=∠C,∠ADB=∠DBC,
∵∠C=∠EBC,
∴∠EBC=∠DBC,
∴BC平分∠DBE.
【解析】(1)求出∠1=∠DBC,根据平行线的判定得出AB∥CF,根据平行线的性质得出∠C=∠EBC,求出∠A=∠EBC,根据平行线的判定得出即可;(2)根据角平分线定义求出∠FDA=∠ADB,根据平行线的性质得出∠FDA=∠C,∠ADB=∠DBC,∠C=∠EBC,求出∠EBC=∠DBC即可.
【考点精析】根据题目的已知条件,利用平行线的判定与性质的相关知识可以得到问题的答案,需要掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:
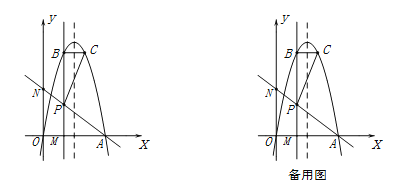
【题目】抛物线![]() 与
与![]() 轴相交于O、A两点(其中O为坐标原点),过点P(2,2a)作直线PM⊥x轴于点M,交抛物线于点B,点B关于抛物线对称轴的对称点为C(其中B、C不重合),连接AP交y轴于点N,连接BC和PC.
轴相交于O、A两点(其中O为坐标原点),过点P(2,2a)作直线PM⊥x轴于点M,交抛物线于点B,点B关于抛物线对称轴的对称点为C(其中B、C不重合),连接AP交y轴于点N,连接BC和PC.
(1)![]() 时,求抛物线的解析式和BC的长;
时,求抛物线的解析式和BC的长;
(2)如图![]() 时,若AP⊥PC,求
时,若AP⊥PC,求![]() 的值;
的值;
(3)是否存在实数![]() ,使
,使![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,它表示甲乙两人从同一个地点出发后的情况.到十点时,甲大约走了13千米.根据图象回答: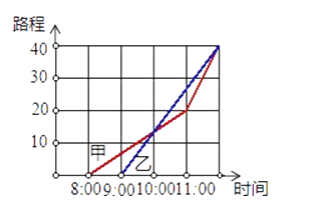
(1)甲是几点钟出发?
(2)乙是几点钟出发,到十点时,他大约走了多少千米?
(3)到十点为止,哪个人的速度快?
(4)两人最终在几点钟相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于A、B两点,B点坐标为(3,0),与y轴交于点C(0,﹣3)
与x轴交于A、B两点,B点坐标为(3,0),与y轴交于点C(0,﹣3)
(1)求抛物线的解析式;
(2)点P在抛物线位于第四象限的部分上运动,当四边形ABPC的面积最大时,求点P的坐标和四边形ABPC的最大面积.
(3)直线l经过A、C两点,点Q在抛物线位于y轴左侧的部分上运动,直线m经过点B和点Q,是否存在直线m,使得直线l、m与x轴围成的三角形和直线l、m与y轴围成的三角形相似?若存在,求出直线m的解析式,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A,B,P在一条直线上,则下列等式中,能判断点P是线段AB中点个数有 ( )
①AP=BP;②.BP= ![]() AB;③AB=2AP;④AP+PB=AB.
AB;③AB=2AP;④AP+PB=AB.
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一件商品先按成本提高50%标价,再以8折(标价的80%)出售,结果仍获利200元,则这件商品的成本是( )
A. 800元 B. 1000元 C. 1600元 D. 2000元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com