
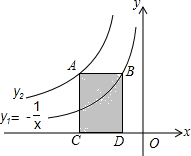
 如图是双曲线y1、y2在第二象限的图象,其中y1=-
如图是双曲线y1、y2在第二象限的图象,其中y1=-| 1 |
| x |
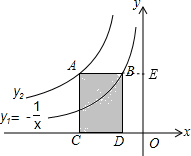
| 3 |
| x |
| 3 |
| x |
| k |
| x |


科目:初中数学 来源: 题型:
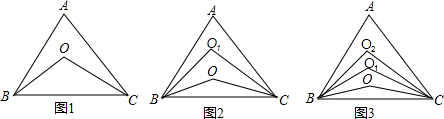
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n |
查看答案和解析>>
科目:初中数学 来源: 题型:
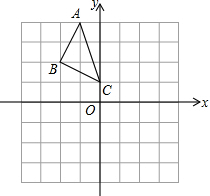 如图,网格图中的每小格均是边长是1的正方形,△ABC的顶点均在格点上,请完成下列各题:
如图,网格图中的每小格均是边长是1的正方形,△ABC的顶点均在格点上,请完成下列各题:查看答案和解析>>
科目:初中数学 来源: 题型:
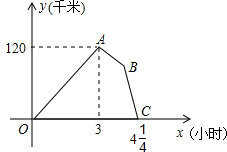 某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后卸完物品再另装货物共用45分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米/时,两车之间的距离y(千米)与货车行驶时间x(小时)之间的函数图象如图所示,下面结论错误的是( )
某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后卸完物品再另装货物共用45分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米/时,两车之间的距离y(千米)与货车行驶时间x(小时)之间的函数图象如图所示,下面结论错误的是( )| A、快递车从甲地到乙地的速度为100千米/时 | ||
| B、甲、乙两地之间的距离为120千米 | ||
C、图中点B的坐标为(3
| ||
| D、快递车从乙地返回时的速度为90千米/时 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com