
【题目】△ABC中,∠BAC>90°,∠ACB=∠ABC=α,点D为BC边上任意一点,点E在AD延长线上,且BC=BE.
(1)当α=30°,点D恰好为BC中点时,补全图1,求∠BEA的度数;
(2)如图2,若∠BAE=2α,此时恰好DB=DE,连接CE,求证:△ABE≌△CEB.

【答案】(1)30°(2)证明见解析
【解析】
(1)只要证明AE⊥BC,△BCE是等边三角形即可解决问题;
(2)如图2中,延长CA到F,使得BF=BC,则BF=BE=BC,连接BF,作BM⊥AF于M,BN⊥AE于N,只要证明Rt△BMF≌Rt△BNE,推出∠BEA=∠F,由BF=BC,推出∠F=∠C=α,推出∠BEA=α即可.
(1)补全图1,如图所示.
∵AB=AC,BD=DC,
∴AE⊥BC,
∴EB=EC,∠ADB=90°,
∵∠ABC=30°,
∴∠BAE=60°
∵BC=BE,
∴△BCE是等边三角形,∠DEB=∠DEC,
∴∠BEA=30°;
(2)延长CA到F,使得BF=BC,则BF=BE=BC,连接BF,作BM⊥AF于M,BN⊥AE于N,
∵∠ACB=∠ABC=α,
∴∠FAB=∠ABC+∠ACB=2α,
∵∠BAE=2α,
∴∠MAB=∠NAB,
∴BM=BN,
在Rt△BMF与Rt△BNE中,
![]() ,
,
∴Rt△BMF≌Rt△BNE(HL),
∴∠F=∠AEB,
∵BF=BC,
∴∠F=∠ACB=α,
∴∠AEB=α,
∴∠ACB=∠AEB,
∴A,B,E,C四点共圆,
∴∠BAE=∠ECB,
在△ABE与△CEB中,
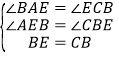 ,
,
∴ABE≌△CEB(AAS).


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:
【题目】已知平行四边形ABCD中,CE平分∠BCD且交AD于点E,A F∥CE,且交BC于点F.
(1)求证:△ABF≌△CDE;
(2)如图,若∠1=65°,求∠B的大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】母亲节即将来临,“花之语”鲜花店准备购买A,B两种鲜花礼盒,A型礼盒每盒成本为40元,售价为65元,B型礼盒每盒成本是60元,售价是100元,
(1)该花店原计划购进两种礼盒共80盒,若全部销售,要使总利润不低于2750元,该花店原计划最多购进多少盒A型礼盒?
(2)为了获得更多的利润,花店负责人决定在实际的销售中将B型礼盒的售价下调![]() ,A型礼盒的价格不变,根据市场情况分析,相应的两种礼盒的销售量与(1)中获得最低利润的销售量相比,A型礼盒的销售量增加了
,A型礼盒的价格不变,根据市场情况分析,相应的两种礼盒的销售量与(1)中获得最低利润的销售量相比,A型礼盒的销售量增加了![]() ,B型礼盒的销售量增加了30盒,这样恰好获得3300元利润,求
,B型礼盒的销售量增加了30盒,这样恰好获得3300元利润,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周六上午,小亮去图书馆查资料,图书馆离家不远,他步行去图书馆,查完资料后他又边走边转去书店买书,在书店停留了几分钟后骑共享单车回家."已知小亮离家的距离![]() (米)与离开家的时间
(米)与离开家的时间![]() (分)之间的关系如图所示.请根据图象回答下列问题:
(分)之间的关系如图所示.请根据图象回答下列问题:
(1)小亮出发几分钟后到达图书馆?
(2)小亮查完资料后步行的速度是多少?
(3)小亮![]() 离开图书馆,几点回到家?
离开图书馆,几点回到家?

查看答案和解析>>
科目:初中数学 来源: 题型:
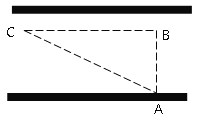
【题目】“道路交通管理条例”规定:小汽车在城街上行驶速度不得超过70千米/小时,如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路面对车速检测仪A正前方30米B处,过了2秒后,测得小汽车C与车速检测仪A间距离为50米,这辆小汽车超速了吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线与x轴交于A(﹣1,0),B(3,0),与y轴交于点C(0,3).
(1)求该抛物线所对应的函数关系式;
(2)设抛物线上的一个动点P的横坐标为t(0<t<0),过点P作PD⊥BC于点D.
①求线段PD的长的最大值;②当BD=2CD时,求t的值;
(3)若点Q是抛物线的对称轴上的动点,抛物线上存在点M,使得以B、C、Q、M为顶点的四边形为平行四边形,请求出所有满足条件的点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,图中的小方格都是边长为1的正方形,
①直接写出△ABC的各顶点坐标:
A(____,___),B(______,_______),C(______,_______);
②画出△ABC关于y轴的对称图形△A1B1C1;
③直接写出△ABC关于x轴对称的△A2B2C2的顶点A2(_____,____)B2(____,____)(其中A2与A对应,B2与B对应,不必画图.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,四边形OABC为矩形,点A的坐标为(4,0),点B的坐标为(4,3),动点M,N分别从O、B同时出发,以每秒1个单位长度的速度运动,其中,点M沿OA向终点A运动,点N沿BC向终点C运动,过点M作MP⊥OA,交AC于P,连接NP.下列说法①当点M运动了2秒时,点P的坐标为(2, ![]() );②当点M运动
);②当点M运动 ![]() 秒时,△NPC是等腰三角形;③当点N运动了2秒时,△NPC的面积将达到最大值.其中正确的有 .
秒时,△NPC是等腰三角形;③当点N运动了2秒时,△NPC的面积将达到最大值.其中正确的有 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接中国森博会,某商家计划从厂家采购A,B两种产品共20件,产品的采购单价(元/件)是采购数量(件)的一次函数,下表提供了部分采购数据.
采购数量(件) | 1 | 2 | … |
A产品单价(元/件) | 1480 | 1460 | … |
B产品单价(元/件) | 1290 | 1280 | … |
(1)设A产品的采购数量为x(件),采购单价为y1(元/件),求y1与x的关系式;
(2)经商家与厂家协商,采购A产品的数量不少于B产品数量的 ![]() ,且A产品采购单价不低于1200元,求该商家共有几种进货方案;
,且A产品采购单价不低于1200元,求该商家共有几种进货方案;
(3)该商家分别以1760元/件和1700元/件的销售单价售出A,B两种产品,且全部售完,在(2)的条件下,求采购A种产品多少件时总利润最大,并求最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com