
科目: 来源: 题型:
【题目】如图,在四边形ABCD中,∠ADC=∠ABC=90°,AD=CD,DP⊥AB于点P.若四边形ABCD的面积是18,则DP的长是( )
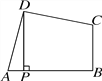
A. 3 B. 2![]() C. 3
C. 3![]() D. 3
D. 3![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】已知,下列n(n为正整数)个关于x的一元二次方程: ①x2﹣1=0,②x2+x﹣2=0,③x2+2x﹣3=0,④x2+3x﹣4=0,…,,…
(1)上述一元二次方程的解为①________,②________,③________,④________.
(2)猜想:第n个方程为________,其解为________.
(3)请你指出这n个方程的根有什么共同的特点(写出一条即可).
查看答案和解析>>
科目: 来源: 题型:
【题目】已知关于x的一元二次方程(a+c)x2+2bx+a﹣c=0,其中a、b、c分别为△ABC三边的长.下列关于这个方程的解和△ABC形状判断的结论错误的是( )
A. 如果x=﹣1是方程的根,则△ABC是等腰三角形
B. 如果方程有两个相等的实数根,则△ABC是直角三角形
C. 如果△ABC是等边三角形,方程的解是x=0或x=﹣1
D. 如果方程无实数解,则△ABC是锐角三角形
查看答案和解析>>
科目: 来源: 题型:
【题目】从2017年起,昆明将迎来“高铁时代”,这就意味着今后昆明的市民外出旅行的路程与时间将大大缩短,但也有不少游客根据自己的喜好依然选择乘坐普通列车;已知从昆明到某市的高铁行驶路程是400千米,普通列车的行驶路程是高铁行驶路程的1.3倍,请完成以下问题:(1)普通列车的行驶路程为________千米;(2)若高铁的平均速度(千米/时)是普通列车平均速度(千米/时)的2.5倍,且乘坐高铁所需时间比乘坐普通列车所需时间缩短3小时,求普通列车和高铁的平均速度.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点P与点 Q 都在y轴上,且关于x轴对称.
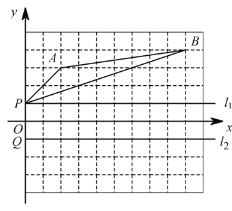
(1)请画出△ABP 关于x轴的对称图形 ![]() (其中点 A 的对称点用
(其中点 A 的对称点用 ![]() 表示,点 的对称点用
表示,点 的对称点用 ![]() 表示);
表示);
(2)点P ,Q 同时都从y轴上的位置出发,分别沿l1,l2方向,以相同的速度向右运动,在运动过程中是否在某个位置使得![]()
![]() 成立?若存在,请你在图中画出此时 PQ 的位置(用线段
成立?若存在,请你在图中画出此时 PQ 的位置(用线段 ![]() 表示),若不存在,请你说明理由(注:画图时,先用铅笔画好,再用钢笔描黑).
表示),若不存在,请你说明理由(注:画图时,先用铅笔画好,再用钢笔描黑).
查看答案和解析>>
科目: 来源: 题型:
【题目】某工程队由甲乙两队组成,承包我市河东东街改造工程,规定若干天完成,已知甲单独完成这项工程所需时间比规定时间多32天,乙队单独完成这项工程所需时间比规定时间多12天,如果甲乙两队先合作20天,剩下的甲单独做,则延误两天完成,那么规定时间是多少天?
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下列材料并回答问题: 材料1:如果一个三角形的三边长分别为a,b,c,记 ![]() ,那么三角形的面积为
,那么三角形的面积为 ![]() . ①
. ①
古希腊几何学家海伦(Heron,约公元50年),在数学史上以解决几何测量问题而闻名.他在《度量》一书中,给出了公式①和它的证明,这一公式称海伦公式.
我国南宋数学家秦九韶(约1202﹣﹣约1261),曾提出利用三角形的三边求面积的秦九韶公式: ![]() . ②
. ②
下面我们对公式②进行变形: ![]() =
= ![]() =
= ![]() =
= ![]() =
= ![]() =
= ![]() .
.
这说明海伦公式与秦九韶公式实质上是同一公式,所以我们也称①为海伦﹣﹣秦九韶公式.
问题:如图,在△ABC中,AB=13,BC=12,AC=7,⊙O内切于△ABC,切点分别是D、E、F.
(1)求△ABC的面积;
(2)求⊙O的半径.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在边长为1的正方形网格中,△ABC的顶点均在格点上,点A、B的坐标分别是A(4,3)、B(4,1),把△ABC绕点C逆时针旋转90°后得到△A1B1C. 
(1)画出△A1B1C,直接写出点A1、B1的坐标;
(2)求在旋转过程中,△ABC所扫过的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了切实关注、关爱贫困家庭学生,某校对全校各班贫困家庭学生的人数情况进行了统计,以便国家精准扶贫政策有效落实.统计发现班上贫困家庭学生人数分别有2名、3名、4名、5名、6名,共五种情况.并将其制成了如下两幅不完整的统计图: 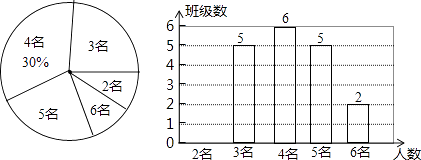
(1)求该校一共有多少个班?并将条形图补充完整;
(2)某爱心人士决定从2名贫困家庭学生的这些班级中,任选两名进行帮扶,请用列表法或树状图的方法,求出被选中的两名学生来自同一班级的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】某商场为了吸引顾客,设立了一个可以自由转动的转盘(转盘被等分成 ![]() 个扇形,如图)并规定:顾客在本商场每消费
个扇形,如图)并规定:顾客在本商场每消费 ![]() 元,就能获得一次转动转盘的机会,如果转盘停止后,指针正好对准红、黄或绿色区域,顾客就可以分别获得 100 元、 50 元、 20 元的购物券.某顾客消费 210 元,他转动转盘获得购物券的概率是多少?他得到 100 元、 50 元、 20 元购物券的概率分别是多少?
元,就能获得一次转动转盘的机会,如果转盘停止后,指针正好对准红、黄或绿色区域,顾客就可以分别获得 100 元、 50 元、 20 元的购物券.某顾客消费 210 元,他转动转盘获得购物券的概率是多少?他得到 100 元、 50 元、 20 元购物券的概率分别是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com