（1）求证：AF=CF；

（2）若∠BAF=35°，求∠BFC的度数．

【题目】如图，已知线段AB=2，MN⊥AB于点M，且AM=BM，P是射线MN上一动点，E，D分别是PA，PB的中点，过点A，M，D的圆与BP的另一交点C（点C在线段BD上），连结AC，DE．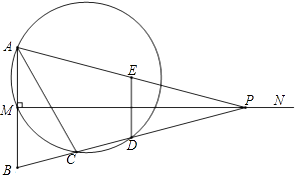

（1）当∠APB=28°时，求∠B和 的度数；
（2）求证：AC=AB．
（3）在点P的运动过程中
①当MP=4时，取四边形ACDE一边的两端点和线段MP上一点Q，若以这三点为顶点的三角形是直角三角形，且Q为锐角顶点，求所有满足条件的MQ的值；
②记AP与圆的另一个交点为F，将点F绕点D旋转90°得到点G，当点G恰好落在MN上时，连结AG，CG，DG，EG，直接写出△ACG和△DEG的面积之比．

（1）在直线BC下方画∠CBE，使∠CBE与∠ABC互补；

（2）在射线BE上任取一点F，过点F画直线FG∥BD交BC于点G；

（3）判断∠BFG与∠BGF的数量关系，并说明理由.

品牌月销售额统计表（单位：万元）

（）该品牌5月份的销售额是 万元；

（）手机部5月份的销售额是 万元；

小明同学观察图1后认为，手机部5月份的销售额比手机部4月份的销售额减少了，你同意他的看法吗？请说明理由；

（）该品牌手机部有A、B、C、D、E五个机型，图2表示在5月份手机部各机型销售额占5月份手机部销售额的百分比情况统计图．则5月份 机型的销售额最高，销售额最高的机型占5月份该品牌销售额的百分比是 ．

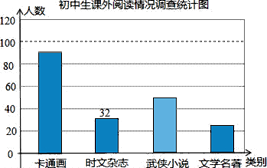
（1）这次随机调查了______名学生，统计表中a=______，d=______；

（2）假如以此统计表绘出扇形统计图，则武侠小说对应的圆心角是______；

（3）试估计该校1500名学生中有多少名同学最喜欢文学名著类书籍？

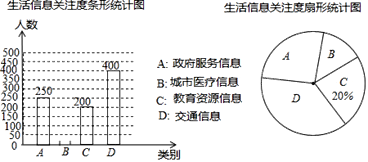
（1）本次参与调查的人数有______ 人；

（2）关注城市医疗信息的有______ 人，并补全条形统计图；

（3）扇形统计图中，D部分的圆心角是______度.

苗苗的画法：

①将含30°角的三角尺的最长边与直线a重合，另一块三角尺最长边与含30°角的三角尺的最短边紧贴；

②将含30°角的三角尺沿贴合边平移一段距离，画出最长边所在直线b，则b//a.

小华的画法：

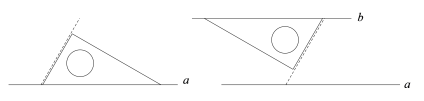
①将含30°角三角尺的最长边与直线a重合，用虚线做出一条最短边所在直线；

②再次将含30°角三角尺的最短边与虚线重合，画出最长边所在直线b，则b//a.

请在苗苗和小华两位同学画平行线的方法中选出你喜欢的一种，并写出这种画图的依据.

答：我喜欢__________同学的画法，画图的依据是__________.

【题目】小黄准备给长8m，宽6m的长方形客厅铺设瓷砖，现将其划分成一个长方形ABCD区域Ⅰ（阴影部分）和一个环形区域Ⅱ（空白部分），其中区域Ⅰ用甲、乙、丙三种瓷砖铺设，且满足PQ∥AD，如图所示．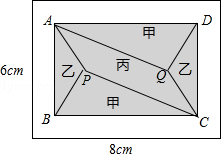

（1）若区域Ⅰ的三种瓷砖均价为300元/m2 ， 面积为S（m2），区域Ⅱ的瓷砖均价为200元/m2 ， 且两区域的瓷砖总价为不超过12000元，求S的最大值；
（2）若区域Ⅰ满足AB：BC=2：3，区域Ⅱ四周宽度相等
①求AB，BC的长；
②若甲、丙两瓷砖单价之和为300元/m2 ， 乙、丙瓷砖单价之比为5：3，且区域Ⅰ的三种瓷砖总价为4800元，求丙瓷砖单价的取值范围．

（1）全班有多少同学？

（2）组距是多少？组数是多少？

（3）跳绳次数x在120≤x＜180范围的同学有多少？占全班同学的百分之几（精确到0.1%）？

【题目】已知：在一条东西向的双轨铁路上迎面驶来一快一慢两列火车，快车长（单位长度）。慢车长（单位长度），设正在行驶途中的某一时刻，如图，以两车之间的某点为原点，取向右方向为正方向画数轴，此时快车在数轴上表示的数是，慢车头在数轴上表示的数是，若快车以个单位长度/秒的速度向右匀速继续行驶，同时慢车以个单位长度/秒的速度向左匀速继续行驶，且与互为相反数.

（1）求此时刻快车头与慢车头之间相距多少单位长度？

（2）从此时刻开始算起，问再行驶多少秒两列火车行驶到车头、相距个单位长度？

（3）此时在快车上有一位爱到脑筋的七年级学生乘客，他发现行驶中有一段时间，他的位置到两列火车头、的距离和加上到两列火车尾、的距离和是一个不变的值（即为定值），你认为学生发现的这一结论是否正确？若正确，求出增定值及所持续的时间；若不正确，请说明理由.

附加题：