
科目: 来源: 题型:
【题目】如图,一个点从数轴上的原点开始,先向右移动3个单位长度,再向左移动5个单位长度,可以看到终点表示的数是-2.已知点A,B是数轴上的点,请参照图并思考,完成下列各题.

(1) 若点A表示数![]() ,将A点向右移动5个单位长度,那么终点B表示的数是 ,此时 A,B两点间的距离是________.
,将A点向右移动5个单位长度,那么终点B表示的数是 ,此时 A,B两点间的距离是________.
(2) 若点A表示数3,将A点向左移动6个单位长度,再向右移动5个单位长度后到达点B,则B表示的数是________;此时 A,B两点间的距离是________.
(3)若A点表示的数为m,将A点向右移动n个单位长度,再向左移动t个单位长度后到达终点B,此时A、B两点间的距离为多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】在我国古代数学著作《九章算术》中记载了一道有趣的数学问题:“今有凫(凫:野鸭)起南海,七日至北海;雁起北海,九日至南海.今凫雁俱起,问何日相逢?”意思是:野鸭从南海起飞,7天飞到北海;大雁从北海起飞,9天飞到南海.野鸭与大雁从南海和北海同时起飞,经过几天相遇.设野鸭与大雁从南海和北海同时起飞,经过x天相遇,根据题意,下面所列方程正确的是( )
A.(9﹣7)x=1
B.(9+7)x=1
C.( ![]() +
+ ![]() )x=1
)x=1
D.( ![]() ﹣
﹣ ![]() )x=1
)x=1
查看答案和解析>>
科目: 来源: 题型:
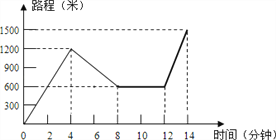
【题目】小红星期天从家里出发汽车去舅舅家做客,当她骑了一段路时,想起要买个礼物送给表弟,于是又折回到刚经过的一家商店,买好礼物后又继续骑车去舅舅家,以下是她本次去舅舅家所用的时间与路程的关系式示意图.根据图中提供的信息回答下列问题:
(1)小红家到学校的路程是______米,小红在商店停留了______分钟;
(2)在整个去舅舅家的途中哪个时间段小红骑车速度最快?最快速度是多少米/分?
(3)本次去舅舅家的行程中,小红一共行驶了多少米?
查看答案和解析>>
科目: 来源: 题型:
【题目】在△ABC中,∠A=90°,AB=4,AC=3,M是AB上的动点(不与A,B重合),过M点作MN∥BC交AC于点N.以MN为直径作⊙O,并在⊙O内作内接矩形AMPN.令AM=x.
(1)用含x的代数式表示△MNP的面积S;
(2)当x为何值时,⊙O与直线BC相切;
(3)在动点M的运动过程中,记△MNP与梯形BCNM重合的面积为y,试求y关于x的函数表达式,并求x为何值时,y的值最大,最大值是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读与理解:
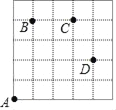
如图,一只甲虫在5×5的方格(每个方格边长均为1)上沿着网格线爬行.若我们规定:在如图网格中,向上(或向右) 爬行记为“+”,向下(或向左) 爬行记为“﹣”,并且第一个数表示左右方向,第二个数表示上下方向.
例如:从A到B记为:A→B(+1,+4),从D到C记为:D→C(﹣1,+2).
思考与应用:
(1)图中A→C( , ),B→C( , ),D→A( , )
(2)若甲虫从A到P的行走路线依次为:(+3,+2)→(+1,+3)→(+1,﹣2),请在图中标出P的位置.
(3)若甲虫的行走路线为A→(+1,+4)→(+2,0)→(+1,﹣2)→(﹣4,﹣2),请计算该甲虫走过的总路程.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB.若DG=3,EC=1,则DE的长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)问题发现
如图1,点E.F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF、则EF=BE+DF,试说明理由;
(2)类比引申
如图2,在四边形ABCD中,AB=AD,∠BAD=90°,点E.F分别在边BC、CD上,∠EAF=45°,若∠B,∠D都不是直角,则当∠B与∠D满足等量关系 时,仍有EF=BE+DF;
(3)联想拓展
如图3,在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠DAE=45°,猜想BD、DE、EC满足的等量关系,并写出推理过程。

查看答案和解析>>
科目: 来源: 题型:
【题目】在进行二次根式化简时,我们有时会碰上如![]() ,
,![]() ,
, ![]() 一样的式子,其实我们还可以将其进一步化简:
一样的式子,其实我们还可以将其进一步化简:
![]() =
=![]() (一),
(一),
![]() (二),
(二),
 (三),
(三),
![]() 还可以用以下方法化简:
还可以用以下方法化简: ![]() =
= (四)
(四)
以上这种化简的方法叫做分母有理化。
(1)请化简![]() =___.
=___.
(2)若a是![]() 的小数部分则
的小数部分则![]() =___.
=___.
(3)矩形的面积为![]() ,一边长为
,一边长为![]() ,则它的周长为___.
,则它的周长为___.
(4)化简![]() .
.
查看答案和解析>>
科目: 来源: 题型:
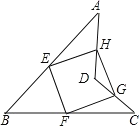
【题目】如图,E. F. G、H分别是边AB、BC、CD、DA的中点.
(1)判断四边形EFGH的形状,并说明你的理由;
(2)连接BD和AC,当BD、AC满足何条件时,四边形EFGH是正方形?证明你的理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:在平行四边形ABCD中,AE⊥BC,垂足为E,CE=CD,点F为CE的中点,点G为CD上的一点,连接DF,EG,AG,∠1=∠2.

(1)求证:G为CD的中点.
(2) 若CF=2,AE=3,求BE的长;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com